Ispravno korištenje stream ciphera nalik RC4

Izvor: SIS Wiki
Skoči na: orijentacija, traži

Sadržaj

Uvod

Kako bi se moglo pričati o pojedinim područjima kriptografije bitno je prvo postaviti temelje, stoga ćemo ukratko započeti sa osnovama kako bi lakše razumjeli srže teme.

Kriptografija je proučavanje i primjena tehnika za sigurno komuniciranje u prisutnosti treće osobe, odnosno, u grubo, primjena i razvoj načina kako trećoj osobi onemogućiti pristup komunikaciji. Kriptografija je jedan od ključnih elemenata na području informacijske sigurnosti budući da je danas informacija definirana kao imovina i ima svoju vrijednost.

Jedna od stručnih definicija kaže: „Kriptografija je proučavanje matematičkih tehnika povezanih sa aspektima informacijske sigurnosti poput povjerljivosti, podatkovnog integriteta, autentikacije entiteta i autentikacije porijekla podataka.[1]“


Četiri temeljna cilja kriptografije, iz kojih proizlaze svi ostali su[2]:

  1. Privatnost ili povjerljivost je usluga koja čuva sadržaj informacije od svih koji nisu autorizirani za njezino posjedovanje.
  2. Integritet podataka je usluga koja se fokusira na ne autoriziranu izmjenu podataka. Kako bi se osigurao integritet trebaju postojati načini otkrivanja manipulacije podacima od treće osobe.
  3. Autentikacija je usluga vezana uz identifikaciju. Ona se veže i uz informaciju i uz entitete, a temelji se na tome da kada dvije strane stupaju u komunikaciju moraju se i identificirati. Iz ovoga proizlaze dvoje glavne klase kriptografije: autentifikacija identiteta i autentifikacija porijekla podataka.
  4. Ne-negiranje je usluga koja onemogućava nekom entitetu da negira prethodne radnje ili obveze. Kada nastanu neslaganja pri negiranja entiteta da je počinio određene akcije, potrebno je imati protumjere za rješavanje takvih situacija.


Stoga je temeljni cilj kriptografije primjereno uvažavanje navedenih područja u teoriji i praksi kako bi se moglo otkriti i spriječiti neprimjerene štetne radnje.

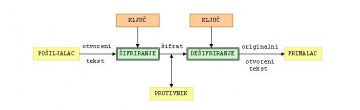
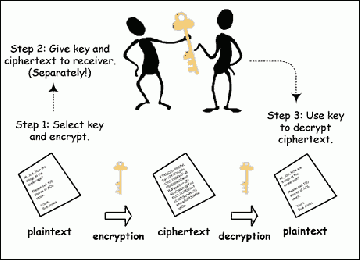
Kako bismo dalje mogli pričati o kriptografiji i njenim primjenama potrebno je definirati temeljne pojmove vezane uz kriptografiju s kojima se susrećemo. Kako je osnovna zadaća kriptografije osigurati neometanu i sigurnu komunikaciju između dva entiteta putem nekog nesigurnog komunkacijskog kanala. Prilikom komunikacije entiteti imaju uloge, od kojih je jedan pošiljalac a drugi primalac. Poruka koja se šalje komunikacijskim kanalom je otvoreni tekst (eng. plaintext) koji može biti bilo kakva vrsta podatka. Kada pošiljalac šalje poruku taj se otvoreni tekst transformira, odnosno šifrira pomoću unaprijed dogovorenog ključa. Tako šifrirana poruka se naziva šifrat (eng. ciphertext) i ona se šalje putem nesigurnog komunikacijskog kanala. Primalac nakon što primi poruku putem ključa dešifrira poruku, te tako dobiva izvorni otvoreni tekst. Umeđuvremenu, ukoliko postoji treći entitet koji želi naštetiti komunikaciji (primjerice pročitati poruku) on će ukoliko ne zna ključ moći vidjeti sadržaj šifrirane poruke, ali neće moći odrediti njen izvorni oblik[3].

Prikaz što je to kriptiranje.
Kriptiranje

Kriptografski algoritam je matematička funkcija koju koristimo za kriptiranje i dekriptiranje, odnosno to su dvije funkcije od kojih jedna obavlja posao kriptiranja a druga dekriptiranja. Te se funkcije odabiru iz određene skupine funkcija ovisno o ključu. Također imamo prostor ključeva koji predstavlja skup svih mogućih vrijednosti ključeva.

Kriptosustavi se u pravilu klasificiraju u skladu sa slijedećim kriterijima[4]:

  1. Tip operacija koje se koriste pri šifriranju
    Pod ovom kategorijom su dvije podjele: supstitucijske šifre i transpozicijske šifre. Kod supstitucijskih šifri se svaki element otvorenog teksta zamijenjuje s nekim drugim elementom, dok kod transpozicijskih šifri se elementi otvorenog teksta permutiraju odnosno premještaju.
  2. Način na koji se obrađuje otvoreni tekst
    Ova se kategorija dijeli na blokovne šifre i protočne šifre. Kod blokovnih šifri se obrađuje jedan po jedan blok elemenata otvorenog teksta korištenjem istog ključa, dok se kod protočnih šifri elementi otvorenog teksta obrađuju jedan po jedan korištenjem niza ključeva koji se paralelno generira.
  3. Tajnost i javnost ključa
    Unutar ove kategorije postoje dvije podjele: simetrični ključevi i kriptosustavi s javnim ključem. Kod simetričnih sustava ključ za dešifriranje se može izračunati poznavajući ključ za dešifriranje i obratno, ali je bitno kako sigurnost takvih sustava leži u tajnosti ključa pa se tako ti sustavi još nazivaju i kriptosustavi s tajnim ključem. Kod kriptosustava s javnim ključem još zvanih i asimetričnih kriptosustava, ključ za dešifriranje se u nekom razumnom vremenu ne može izračunati iz ključa za šifriranje. Kod ovakvih sustava je ključ za šifriranje javan, te svatko njime može šifrirati poruku dok ju jedino entitet koji posjeduje tajni, odnosno privatni ključ može dešifrirati.

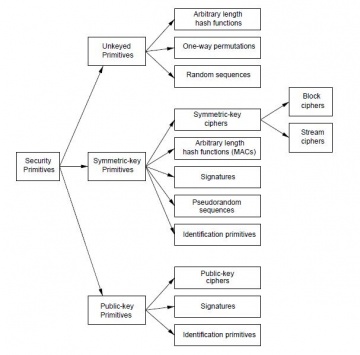
Kao osnova kriptografije su osnovni kriptografski alati, odnosno Cryptographic primitives[5], kao dobro uspostavljeni kriptografski algoritmi niže razine koji se učestalo koriste za igradnju sustava za računalnu sigurnost. To zapravo znači da se prilikom izgradnje sustava zaštite programeri koriste ovim algoritmima kao osnovama i temeljima za daljnju izgradnju kompleksnijeg sustava budući da su osmišljeni na način da izvršavaju jednu određenu radnju ali sa visokim postotkom pouzdanosti. Postoji nekoliko osnovnih kriptografskih primitiva poput hash funkcija, blok šifri i protočnih šifri.

Cryptographic primitives taksonomija.
Cryptographic primitives taksonomija

Ovi se algoritmi procjenjuju prema nekoliko kriterija:

  1. Stupanj sigurnosti, budući da je to često teško odrediti on se definira nekom gornjom granicom vezanom za količinu rada potrebnog za osvajanje nekog cilja.
  2. Funkcionalnost, ovi se algoritmi u konačnici kombiniraju kako bi se postigli razni sigurnosni ciljevi, stoga funkcionalnost prikazuje koji od ovih algoritama prema svojim svojstvima najviše odgovara zadanom cilju.
  3. Metode rada, prikazuju kako algoritmi ovisno o ulaznim podacima i primjenama u različitim situacijama ostvaruju različite funkcionalnosti, odnosno način rada.
  4. Učinak, prikazuje učinkovitost pojedinog algoritma u nekom određenom načinu rada.
  5. Lakoća implementacije, se odnosi na stupanj težine integracije algoritma u praktičnu primjenu.

--Jelena Valčić 20:17, 19. siječnja 2013. (CET)

Algoritmi sa asimetričnim ključem

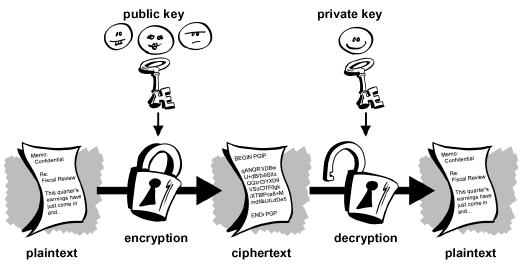
Asimetrično kriptiranje je sustav koji se odnosi na posjedovanje dva ključa za svaku osobu, jedan javni, a drugi tajni. Ta dva ključa su povezana matematičkom funkcijom, i generirani su od istog algoritma, koji vraća dva povezana ključa. Javni ključ služi za kriptiranje poruke, i pomoću njega se ne može dekriptirati poruka zaključana tim istim javnim ključem. Takva poruka se može dekriptirati samo odgovarajućim tajnim ključem. Budući da su ti ključevi matematički povezani, isto vrijedi i suprotno, poruka kriptirana tajnim ključem se može dekriptirati javnim ključem. Ovo se u praksi ne radi, jer javni ključ je najčešće dostupan svima, te bi svi mogli pročitati tu poruku. Ovakav pristup kriptiranju omogućuje sigurnu razmjenu informacija između dvije strane, bez da se prije toga mora razmijeniti ključ (kao kod simetričnog kriptiranja). Štoviše, ovim putem se najčešće i šalje ključ koji se koristi u simetričnom kriptiranju.[6]

Osnovni algoritam rada

Jednostavni grafički primjer:

Jednostavan primjer asimetričnog kriptiranja.
Prikaz kriptiranja javnim ključem i dekriptiranja privatnim ključem.

Praktična uporaba

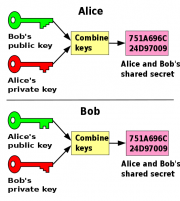
Simetrični sesijski ključ
Prikaz algoritma za stvaranje zajedničkog simetričnog ključa pomoću javnog i tajnog ključa.

Ovaj algoritam se u praksi intezivno koristi, radi toga što nije potrebno prethodno razmijeniti nikakve informacije (kao što kod simetričnog moramo razmijeniti tajni ključ), te se vrlo lako može uspostaviti veza. Jedan od najčešćih primjena ovog algoritma je Diffie-Hellmanova razmjena ključeva. U toj razmjeni Boris uzima svoj privatni ključ i Natašin javni ključ, te ih spaja i time dobije jedan unikatan ključ. Nataša ponavlja isti proces sa svojim privatnim ključem, i Borisevim javnim ključem. Budući da su ti parovi ključeva međusobno povezani matematički, rezultirajući ključevi će se podudarati. Time su Boris i Nataša stvorili unikatan simetričan ključ, pomoću kojeg mogu razmijenjivati poruke bez sa totalnom sigurnošću, pod uvjetom da netko ne sazna jedan od njihovih privatnih ključeva.[7]

Autentifikacija

Autentifikacija kod ovakvog načina razmjene poruka se vrši digitalnim potpisom. Digitalni potpis je metoda verifikacije poruke koja se također vrši sa parom ključeva. Ako Nataša želi poslati potpisanu poruku m Borisu, njen javni ključ označimo kao (n, e), a eksponent dekriptiranja sa d, tada se potpisana poruka izračunava primjenom dekriptirajućeg algoritma na poruku m, i dobivamo s = m^d kao potpisanu poruku. Tada Boris preuzima tu poruku skupa sa njenim potpisom (m, s), i koristeći Natašin javni ključ e izračunava s^e. Ako je s^e jednak poruci m koju je dobio, to znači da je poruka prenesena bez greške, i da je ispravna. Primjenom digitalnom potpisa prije kriptiranja poruke javnim ključem od osobe kojoj želimo poslati poruku se istovremeno zaštiti i potpiše poruka, čime se osigurava da osoba kojoj šaljemo poruku može biti sigurna da smo to mi.[8]

Primjena u praksi

Ova vrsta enkripcije se koristi u mnogim tehnologijama, pa ćemo navesti samo par poznatijih: TLS, PGP i GPG.

TLS (Transport Layer Security) je protokol koji osigurava sigurnost na transportnoj razini u mreži.[9] TLS radi na slijedećem principu:

PGP koristi sličan princip, gdje se generira simetrični ključ koji vrijedi samo za trenutnu sesiju, i šalje se pomoću asimetričnog kriptiranja, ali inkorporira sustav provjere i certifikacije javnih ključeva, gdje se može pratiti tko je sve potpisao određeni javni ključ, te time i vjerodostojnost tog javnog ključa. Najčešće se traže potpisi vjerodostojnih entiteta, sve do najviše razine, na kojoj se nalaze posebne organizacije koje izdaju certifikate za javne ključeve.[10] GPG je PGP sustav koji se nalazi pod GNU General Public License.[11]
--Branimir Jurić 22:25, 20. siječnja 2013. (CET)

Algoritmi sa simetričnim ključem

Kriptiranje sadržaja simetričnim ključem osigurava korisnicima tajnost podataka. Za primjer uzmimo dvije osobe, Alice i Bob koji nastoje komunicirati. Treća strana (Ivan) koja presreće njihove poruke ne bi trebala saznati ništa korisno iz njihovog sadržaja, što je bit kriptiranja općenito. Kako bi osigurali siguran komunikacijski kanal, Alice i Bob se prvo moraju složiti oko nekog ključa k. Ovaj dijeljeni ključ k mora biti tajan. Prije nego što pošalje poruku m (message) Bobu, Alice kriptira m koristeći algoritam E i ključ k. Dobije kriptotext (eng. ciphertext) c = E (k,m) te pošalje c Bobu. Koristeći dekripcijski algoritam D i isti ključ k, Bob dekriptira c te tako dolazi do izvornog teksta (eng. plaintext) m = D (k,c). Iz ovoga primjera se vidi zašto se ovaj tip kriptiranja naziva simetričnim – obje strane koriste isti ključ, k za kriptiranje i dekriptiranje sadržaja. Algoritmi kriptiranja E i dekriptiranja D su javno poznati te svi mogu dekriptirati kriptotekst ukoliko poznaju ključ. Ukoliko Alice i Bob žele da njihova poruka ostane tajna, moraju nekako zadržati ključ k tajnim. Na sljedećoj slici je vidljivo kako bi to pojednostavljeno izgledalo:

Jednostavan primjer simetričnog kriptiranja.
Simetrično kriptiranje - isti ključ za kriptiranje izvornog teksta i dekriptiranje kriptoteksta.


Upravo tu leži glavni problem simetričnog ključa, Alice i Bob se moraju složiti oko ključa k na siguran i efikasan način. Za razmjenu ključa potrebne su metode kriptografije javnog ključa, o kojima nešto kasnije. Potrebno je da se kriptirani tekst m može na jedinstveni način dobiti iz kriptoteksta c, što znači da za ključ fiksne duljine k, mapa kriptiranja mora biti bijektivna (injektivna i surjektivna), što bi (matematički govoreći) izgledalo ovako:

E∶KxM→C takav da je za svaki k∈K mapa E_k ∶M→C,m→E(k,m) invertibilna.

Elementi m∈M predstavljaju poruke (plaintext). C je set kriptotekstova ili kriptograma, elementi k∈K su ključevi. E_k se naziva funkcija kriptiranja sa obzirom na ključ k. Inverzna funkcija D_k≔E_k^(-1) se zove funkcija dekripcije. Pretpostavlja se da efikasni algoritmi koji računaju spomenute funkcije postoje. Osnovi sigurnosni zahtjev za mapu kriptiranja E je da , bez poznavanja ključa k, ne bi smjelo biti moguće uspješno izvršiti funkciju dekripcije. Od svih algoritama kriptiranja, algoritmi sa simetričnim ključem se najbrže implementiraju hardverski i softverski. Upravo iz tog razloga se koriste za kriptiranje velike količine podataka. Da bi Alice i Bob sigurno razmjenili poruke, moraju prvo razmijeniti ključ k preko sigurnog komunikacijskog kanala, za što se često koriste metode kriptiranja sa javnim ključem. Iz ovoga zaključujemo da se te dvije spomenute metode trebale koristiti zajedno kako bi izgradili praktične kriptosustave. 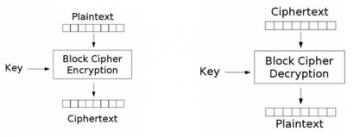Kada se govori o algoritmima kriptiranja sa simetričnim ključem, obično se spominju blok šifre i stream šifre. Funkcija kriptiranja koja koristi blok šifru obrađuje tekst fiksne duljine dok stream šifra radi na slijedu (toku) teksta obrađujući znak po znak kriptira tekst proizvoljne duljine. Ukoliko tekst prelazi veličinu bloka u blok šifri, koriste se razne operacije od kojih neke koriste i stream šifre. --Ljubarac 19:45, 19. siječnja 2013. (CET)


Blok šifre

Blok šifra koristi tajni ključ k binarne duljine r, algoritam kriptiranja E kriptira blokove teksta m fiksne binarne duljine n te rezultirajući blokovi kriptoteksta c = E (K,m) također imaju duljinu n. n se naziva blok duljina šifre. Tipične blok duljine su 64 (DES) ili 128 (AES), tipična duljina ključa je 56 (DES), 128, 192, 256 (AES) ili 512 (SHACAL2).

Jednostavan primjer blok simetričnog kriptiranja.
Blok šifra - jednostavna shema.

Pogledajmo sada blok šifru E sa duljinom bloka n i ključem duljine r. Postoji 2^n blokova teksta te 2^n blokova kriptoteksta duljine n. Za ključ fiksne duljine k, funkcija kriptiranja Ek : m -> E (k,m) mapa {0,1}^n bijektivnih sa {0,1}^n je permutacija (mapa f : D -> D se naziva permutacija od D ukoliko je f bijektivan) od {0,1}^n. Dakle, izabrati ključ k znači izabrati permutaciju od Ek od {0,1}n te se zatim ta permutacija koristi da se kriptiraju blokovi teksta. 2n permutacija Ek , sa k koji prolazi kroz set od {0,1}r ključeva, formiraju gotovo zanemarivo mali podset u velikom setu svih permutacija {0,1}^n, koji se sastoji od 2^n! elemenata. Zato se nasumično bira r-bitni ključ k za E te se zatim ograničava selekcija permutacije kriptiranja na ekstremno mali podset. Iz prethodnoga bi trebali moći zaključiti da ne možemo imati idealnu blok šifru sa savršenom tajnošću u praksi. Maksimalna razina sigurnosti blok šifre znači i maksimalnu slučajnost (dok se bira slučajni bit ključa), što znači da, dok biramo ključ, moramo uzeti slučajni element iz seta svih permutacija od {0,1}n. Ovo se u praksi pokazalo iznimno nepraktično, što i (napokon) ima nekog smisla. Mogli bi pokušati pobrojati sve permutacije te onda nasumično uzeti indeks (koji bi bio ključ).

Prisjetimo se da postoji 2^n! permutacija, što bi značilo da moramo negdje spremiti sve te brojeve. Za blok šifru duljine n od 64 bita, trebali bi 267 byteova da bi spremili jedan ključ, što je izrazito nepraktično (gotovo nemoguće). U praksi se stoga ograničavamo na mnogo manje ključeve i biramo permutaciju kriptiranja Ek za ključ k iz mnogo manjeg seta od 2r permutacija, sa r koji je obično u rasponu od 56 do 256. Ideja je i dalje ista – doći do funkcije kriptiranja koja se ponaša kao nasumično izabrana funkcija za jako veliki set svih permutacija. Najpoznatiji algoritmi sa blok šifrom su DES (3DES) te AES koji se ovdje neće detaljno spominjati. --Ljubarac 19:45, 19. siječnja 2013. (CET)


Protočne šifre (stream ciphers)

Generator slučajnih brojeva (eng. random generator) je drugi osnovni kriptografski primitiv. Poznad je i pod nazivom keystream generator ili stream cipher (protočna šifra). Također je i slučajna funkcija, ali za razliku od hash funkcija ima manji ulaz i duži izlaz. Na konceptualnoj razini, stream šifru promatramo kao pronalazak slučajnih brojeva čija je duljina fiksna dok je duljina izlaza dugački niz bitova, poznat kao keystream. U praksi se može koristiti kako bi se jednostavno zaštitila povjerljivost backup podataka; iskoristimo generator toka ključeva, upišemo ključ, dobijemo datoteku sa slučajnim bitovima, i XOR-amo ih sa izvornim tekstom da bi dobili kriptotekst. Ukoliko trebamo doći do izvornih podataka, vratimo se do generatora, unesemo isti ključ, dobijemo datoteku sa slučajnim podacima, XOR-amo ih sa kriptotekstom i dobijemo izvorni tekst. Matematički, protočne šifre bi se definirale kao:

Neka je K set ključeva i M set izvornih tekstova. U ovom kontekstu, elementi M se nazivaju znakovima. Protočna šifra (stream cipher)

E* ∶ K* x M*→ C*,E* (k,m)≔c≔c_1 c_2 c_3…

kriptira tok (eng. stream) m := m1 m2 m3... ∈ M* znakova izvornog teksta m_i ∈ M kao tok c∶= c_1 c_2 c_3… ∈ C* znakova kriptoteksta c_i ∈ C koristeći tok ključeva (keystream) k∶= k_1 k_2 k_3… ∈ K*),k_i ∈ K.
Tok izvornog teksta se kriptira znak po znak. Za ovu svrhu postoji mapa kriptiranja

E ∶ KxM→C,

koja kriptira jedan znak izvornog teksta mi sa odgovarajućim znakom ključa k_i

c_i=E(k_i,m_i ),i=1,2,3…

Obično su znakovi iz M i C te elementi ključa K binarne znamenke. Dekriptiranje se također vrši znak po znak koristeći funkciju dekripcije D sa istim tokom ključeva (keystream) koji se koristio za kriptiranje. Većina protočnih šifri koristi binarni XOR operator. --Ljubarac 19:45, 19. siječnja 2013. (CET)


RC4

RC4 je jedna vrsta protočnih šifri, također veoma popularna, razvijena od Ron Rivesta iz RSA Data Security Inc. Koristi se u sklopu brojih aplikacija, a jednu od najvažnijih uloga ima u SSL-u koji se koristi za sigurnost većine svjetskog elektroničkog poslovanja preko interneta. Također je primjenu našao i u WEP-u, IEEE-ovom standardu za sigurnost bežične mreže, te u aplikacijama koje uključuju e-mail kriptiranje.

RC4 je binarno dodavajuća protočna šifra. Koristi ključ varirajuće veličine u rasponu od 8 do 2048 bita u višekratnicima od 8 bita. To zapravo znači da je srž algoritma sadržana u funkciji koja generira tok ključeva. Ta funkcija generira sekvencu bitova koji se kombiniraju sa otvorenim tekstom pomoću XOR metode. Dekripcija funkcionira na način da se regeneriratok ključeva koje se zatim putem XOR metode kombinira sa kriptiranim tekstom. Drugi bitan dio algoritma je inicijalizacijska funkcija koja prihvaća ključ varirajuće veličine, te ga koristi kako bi inicijalizirala početno stanje generator toka ključeva. Ta se funkcija još naziva algoritam rasporeda ključeva.

Ovaj algoritam je zapravo skup algoritama koji za parameter imaju veličinu bloka, gdje je taj n parameter veličina riječi za taj algoritam. Preporučeno je da on bude jednak 8, doduše za svrhe analiziranja može biti i manji, a ukoliko se želi dodatna sigurnost taj se parameter može i povećati. Unutarnja stanje RC4 algoritma se sastoji od tablice veličine 2^n riječi i dva brojača koji su veličine jedne riječi. Tablica se zove S-box, te uvijek sadrži permutaciju mogućih 2^n vrijednosti riječi[12].

U nastavku je prikazan algoritam rasporeda ključa u RC4. Unutar algoritma varijabla S predstavlja S-box tablicu, K je skup ključeva dok su i i j brojači. Algoritam prihvaća kao ulazni podatak ključ koji je pohranjen u K i duljine je l bajtova. Zatim započinje permutaciju identiteta u S, te korištenjem ključa neprestano zamijenjuje vrijednost kako bi dobio nove nepoznate permutacije koje su ovisne o ključu[13]. 

Inicijalizacija:
 For (i = 0 do 2n – 1)
      S[i] = i
 j = 0




Izmjena:
 For ( i = 0 do 2n – 1)
	j = j + S[i] + K[i mod l]
	Zamijeni(S[i], S[j])


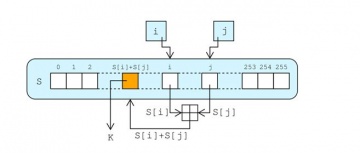
Generator toka ključeva unutar RC4 je prikazan slijedećim pseudokodom. On neprestano izmjenjuje premutacije pohranjene unutar varijable S u svakom slijedećem krugu birajući drugačiju vrijednost iz S permutacija kao izlaznu informaciju. Jedna iteracija RC4 algoritma kao izlaz daje n bitnu riječ kao tok ključeva koji se tada može pomoću XOR metode kombinirati sa otvorenim tekstom kako bi se dobio kriptirani tekst[14]. 

Inicijalizacija:
 i = 0
 j = 0


Generirajuća petlja:
 i = i + 1
 j = j + S[i]
 Zamijeni(S[i], S[j])
 Izlaz z = S[ S[i] + S[j] ]
Pseudo-slučajni generator.
Prikaz iteracije unutar generatora toka ključeva

U svakoj iteraciji pseudo-slučajni generator se povećava za vrijednost i i traži i-ti element unutar S, odnosno S[i] te ga zbraja sa j. Zatim zamjenjuje vrijednosti S[i] i S[j] i zbroj vrijednosti S[i] + S[j] (modulo 256) koristi kao indeks kako bi dohvatio treći element od S (vrijednost toka ključeva K) koji se zatim metodom XOR kombinira sa slijdećim bajtom poruke kako bi dobio slijedeći bajt otvorenog teksta ili kriptiranog teksta. Tokom ovog procesa se svako element od S zamijenjuje sa nekim drugim elementom barem jednom unutar 256 iteracija[15].


Ključne stvari kod RC4[16]: 


import sys

#KSA - Key-Scheduling Algorithm (wiki)
def KSA(kljuc):

    duljina_kljuca = len(kljuc) #predstavlja broj bajtova u kljucu
    S = range(256) #postavljanje permutacija identiteta
    
    j = 0
    
    for i in range (256):

        j = (j + S[i] + kljuc[i % duljina_kljuca]) % 256
        S[i], S[j] = S[j], S[i] #zamjena vrijednosti

    return S


#PRGA - Pseudo-Random Generation Algorithm (wiki)
def PRGA(S):

    i = 0
    j = 0

    while True:

        i = (i + 1) % 256
        j = (j + S[i]) % 256
        S[i], S[j] = S[j], S[i] #zamjena vrijednosti
        K = S[(S[i] + S[j]) %256] #bajt toka kljuceva
        

        yield K #yield se ovdje koristi jer je pogodniji za generatore

def RC4(kljuc):
    S = KSA(kljuc)
    return PRGA(S)


def konverzija_kljuca(v_k):
    return [ord(c) for c in v_k]



def kriptiraj(text, k):

    kljuc = konverzija_kljuca(k)
    tok_kljuceva = RC4(kljuc)


    for c in text:
        sys.stdout.write("%02X" % (ord(c) ^ tok_kljuceva.next()))
    print

Kod se temelji na primjeru implementacije koji se može naći na RC4 wiki[17] i Learning Python by example: RC4[18] te prikazuje jednostavno korištenje RC4 algoritma za kriptiranje, također su se koristili testni podaci priloženi na wiki stranici:

Ključ Tok ključeva Otvoreni tekst Kriptirani tekst 
Key
 
EB9F7781B734CA72A719...
 
Plaintext
 
BBF316E8D940AF0AD3
 
Wiki
 
6044DB6D41B7...
 
pedia
 
1021BF0420
 
Secret
 
04D46B053CA87B59...
 
Attack at dawn
 
45A01F645FC35B383552544B9BF5

Izvorni kod se može naći ovdje[19] --Jelena Valčić 21:02, 19. siječnja 2013. (CET)

Ranjivosti šifri sličnih RC4

Šifre slične RC4 su ranjive na niz problema već po svom dizajnu. Neke od njih su već spomenute u prethodnom tekstu, ovdje su objašnjene ostale šifre.

Ranjivosti temeljene na PRG algoritmu

PRG algoritam generira ključeve koji se koriste u RC4 algoritmu. Budući da je taj algoritam jednostavan, postoji nekoliko načina za probijanje šifre.
Pogađanje stanja
Pogađanje stanja se bazira na tome da se pogodi mali dio početnog stanja RC4 generatora ključa (PRG), te da se paralelno vrti algoritam. Ako u bilo kojem trenutku dođe do kontradikcije u dobivenim ključevima (ključ koji je izgenerirao RC4 je drukčiji od ključa kojeg mi usporedno generiramo), moguće je otkriti gdje je greška u inicijalnoj pretpostavci, i krenuti ispočetka sa ispravljenom greškom. Nakon određenog broja prolaza se otkrije početni ključ, a dalje je trivijalno naći bilo koju izvedenicu.
Pristranost prema drugom byteu
Ako je treći byte orginalnog stanja nula, a drugi byte nije 2, tada je vjerovatnost da je drugi byte u šifri jedan 0 duplo veća nego što bi trebala biti (1/128 umjesto 1/256). To znači da ako je vrijednost drugog bytea jednaka nula, može se pretpostaviti vrijednost trećeg byte početne vrijednosti sa vjerovatnošću 1/2, što se onda može iskoristiti za pogađanje stanja.[20]

Ranjivosti temeljene na ključu

Neke ranjivosti iskorištavaju ključeve koji se koriste u RC4 algoritmima, da probiju šifru preko nekih njihovih svojstava.
Analiza sličnih ključeva
Neki ključevi su povezani na određeni način, te daju sličan izlaz za prvih par izlaznih byteova. To je dokazano tako da se uspoređuju dva ključa, koji se razliku u samo jednom byteu (t). Dok god radimo t-1 iteracija, ključevi i stanje će biti isti. Tek na t koraku će se izmjeniti stanja, i razlikovat će se u dva bytea. Ako se t nalazi u početnih par byteova, tada će se stanja jako brzo razlikovati, ali ako se t nalazi pri kraju 2n, tada će se početna stanja podudarati u većinskom dijelu.
Pristranost izlaza prema ključu
Određeni ključevi su okarakterizirani kao slabi, to jest, da imaju neka svojstva koja ih čine ranjivima na napade. Dio takvih slabih ključeva je takvog oblika da neki njihov podset potpuno određuje podset izlaznih bitova. Za određene vrijednosti takvih ključeva čak možemo dobiti i da njihov određen podset potpuno određuje veliku većinu bitova izlaznog stanja.[21]
Ranjivosti temeljene na inicijalizacijskom vektoru (WEP)
WEP koristi IV (inicijalizacijski vektor) od 3 bytea, koji se dodaje ključu da stvori sesijski ključ. Prilikom razmjena podataka između wireless routera i klijenta podatci se šifriraju sa RC4 algoritmom, koji uzima sesijski ključ. Budući da sesijski ključ sadrži IV, razumno je pretpostaviti da će se IV slati mnogo puta, ako postoji nekakav promet sa routerom. Ako pretpostavimo da se IV konstatno mijenja, to ne predstavlja nikakav problem. Ali kod WEP-a to nije slučaj. Inicijalizacijski vektor je najčešće uvijek isti, nekad čak i na različitim routerima (ovisi o proizvođaču). Pod pretpostavkom da se podatci konstatno razmjenjuju, to znači imamo 24 bita (3 bytea) ključa koji su uvijek konstatni u svakom paketu. Nakon presretanja dovoljnog broja poruka se može odrediti koji su to točno dijelovi paketa. IV se automatski stavlja uvijek na isto mjesto, ili na početak ili na kraj tajnog ključa. Tada se jako lako može prethodnim metodama pronaći cijeli ključ, a preko njega i početno stanje, što je u ovom slučaju lozinka za pristup mreži. Ovaj propust se lako rješava, hashiranjem IV sa ključem, umjesto da se IV samo dodaje na ključ.
--Branimir Jurić 22:25, 20. siječnja 2013. (CET)

Ispravno korištenje šifri nalik RC4

Korištenje šifri nalik RC4 (i same RC4 šifre) sigurno je problematično. Ne možemo biti potpuno sigurni kako bi općenito upotrebljavali RC4, zbog teoretskih slabosti koje su objašnjene u prethodnim poglavljima. Ipak, RC4 i druge šifre nalik RC4 je moguće koristiti ispravno. Počnimo od najjednostavnijih problema koji se susreću pri korištenju PRG-baziranih šifri (pseudo random generator) nalik RC4. Očito je da se ne smije koristiti isti tok ključeva (keystream) da se kriptiraju dvije različite poruke.


Problem sa PRG baziranim šiframa

Iako je prethodno možda i (pre)očito, Microsoft je učinio upravo to u Office paketu 2007. godine [22], kriptirajući više verzija Word dokumenta sa istim ključem. Ukoliko se baš mora koristiti isti ključ, rješenje je kombinirati ga sa inicijalizacijskim vektorom (IV) ili „nonce“ [23]. Naravno, to može također biti problematično, kao kod WEP-a[24]. Još jedan veliki problem je – ukoliko se obrne bit u RC4 kriptotekstu, isti bit u dekriptiranom izvornom tekstu će se također obrnuti što može voditi do praktičnih „padding-oracle“ [25] napada koji kompromitiraju sigurnost kriptosustava. Rješenje ovog problema bi bilo korištenje MAC-a (eng. message authentication code) na kriptotekstu kako bi se isti autentificirao.

Problem sa Key Scheduling Algoritmom (KSA)

Navjeći problem KSA algoritma RC4 šifre je njegova jednostavnost. Pogledajmo jednu implementaciju:

for i from 0 to 255
S[i] = i endfor
j = 0

for i from 0 to 255
j = (j + S[i] + key[i mod keylength]) mod 256
swap values of S[i] and S[j]
endfor

KSA se koristi kako bi se inicijalizirana permutacija u listi S. Duljina ključa (keylength) se definira kao broj byteova u ključu i može biti u rasponu od 1 do 256, tipično između 5 i 16, što odgovara duljini ključa 40-128 bitova. S se obrađuje kroz 256 iteracija na način prikazan u kodu. KSA jednostavno nije dovoljno nepredvidljiv. Usporedimo to sa novim špilom karata. Počevši od nepromiješanog špila, sistematski radimo od vrha prema dnu mijenjajući poziciju svake karte sa drugom kartom u špilu. Pozicije koje se mijenjaju su određene sa nekoliko jednostavnih računskih operacija koje uključuju vrijednost originalne karte i kriptografski ključ. Ukoliko se isto napravi sa pet špilova karata, dobije se nešto slično RC4 KSA.

Najpoznatiji napad na RC4 KSA

FMS (Fluhrer, Mantin i Shamir) napad se prvi put pojavio 2001. godine. Promatrao je KSA za koji je otkriveno da je za neke slabe ključeve prvi byte izlaza PRGA povezan sa byteovima ključa. Ovaj napad savršeno radi kod implementacija koje dodaju poznati inicijalizacijski vektor (IV) na WEP ključ. Promatrajući nekoliko milijuna IV-a , napadač može skupiti dovoljno tokova ključa (keystream) kako bi došao do šifre. Rješenje problema FMS-a bi bilo:

Efikasnost prve metode je diskutabilna. Drugu metodu je usvojio WPA-TKIP. Kao hash funkcija TKIP se nije pokazao najprikladnijim. Preporuka je da se za RC4 koristi bolji hash algoritam kao SHA-256 kako bi se hashirao IV i ključ.

Da li se šifre kao RC4 mogu koristiti ispravno?

Ukratko – mogu. Potrebno je koristiti dobru hash funkciju koja će hashirati inicijalizacijski vektor (IV) i ključ i/ili izbacivanje prvih N byteova i MAC. Ove mehanizme zaštite treba adekvatno koristiti kako bi bili efikasni. Držeći se osnovnih sigurnosnih preporuka te mehanizama zaštite, moguće je ispravno koristiti algoritme kao RC4. Pogledajmo jednostavnu implementaciju nekih od mehanizama zaštite (uz napomenu da je implementacija urađena samo za primjer, ima svoje greške i ne preporučujem da koristite sljedeći kod :D). Skripta je rađena u Python programskom jeziku. 

def crypt(data, key):
   
    j = 0
    S = range(256)
    for i in range(256):
        j = (j + S[i] + ord(key[i % len(key)])) % 256
        S[i], S[j] = S[j], S[i]

    j = i = 0
    out = [] 

    for i in xrange(1024):
        i = (i + 1) % 256
        j = (j + S[i]) % 256
        S[i], S[j] = S[j], S[i]


    for char in data:
        i = (i + 1) % 256
        j = (j + S[i]) % 256
        S[i], S[j] = S[j], S[i]
        out.append(chr(ord(char) ^ S[(S[i] + S[j]) % 256]))  

    return ''.join(out)

Prvi dio se odnosi na standardnu implementaciju RC4 algoritma koji je javan. Pseudokod i informacije o algoritmu su javno dostupne na wiki sustavu[26], a kako implementirati algoritam je tema koja je obrađena u jednom od prethodnih poglavlja. Funkcija crypt , dakle, sadrži KSA i PRGA RC4 algoritma koji su također obrađeni u jednom od prethodnih poglavlja. U sljedećem dijelu koda se nalazi funkcija encrypt koja prima dva argumenta: data (izvorni tekst, plaintext te key (ključ). Sve je base64 enkodirano radi jednostavnosti. 

def encrypt(data, key, encode=base64.standard_b64encode, salt_length=16):
	
	
	# HMAC za provjeru autenticnosti i integriteta podataka
	# moze se i generirati slucajni mackey
	# preporuka: ne koristiti isti kljuc za kriptiranje i mac!
	# ovdje se koristi. neka je. 
	
	mackey = key
	
	salt = os.urandom(salt_length) #random salt duljine 16

	# Hash SHA512
	key = hashlib.sha512(key + salt).digest() #hashiramo kljuc zajedno sa salt
	
	# kriptiranje		
	data = chr(salt_length) + salt + crypt(data, key) #nisam siguran da je ok

	if encode:
		data = encode(data)	    

	# HMAC (sha512)
	check = hmac.new(mackey, data, hashlib.sha512).digest()
	check = encode(check)
	
	# print len(check) #da se sjetim duljine u base64 -.-
	
	data = data + check

	return data

Ovdje se koristi SHA512, salt duljine 16 te MAC (HMAC) mehanizam zaštite. HMAC se koristi za provjeru autentičnosti i integriteta podataka [27]. HMAC se dodaje na kraj hashiranih podataka te će se koristiti u decrypt funkciji. Odmah je moguće primjetiti i grešku - za HMAC se koristi isti ključ kao i za kriptiranje podataka RC4, što nikako nije preporučljivo. Sljedeća funkcija služi kako bi se sadržaj dekriptirao: 

def decrypt(data, key, decode=base64.standard_b64decode):
	
	mackey = key
	
	# 88 bytes za mac provjeru koji smo dodali na kraj (check)
	# base64 encodano je 88 '-.-
	
	mac = data [(len(data) - 88):] # koji dio podataka je check
	data = data [0: (len(data) - 88)] # a koji zapravo podaci
	
	# provjera HMAC
	check = hmac.new(mackey, data, hashlib.sha512).digest() #ponovno racunanje provjere
	mac = decode(mac) #dekodiranje iz base64 za provjeru
	
	if check != mac: # ponovno kreirani mac razlicit od dohvacenog?
	    print 'Manipulirana poruka ili krivi kljuc!'
	
	elif decode:
	    data = decode(data)
		
	pos = ord(data[0]) + 1
	salt = data[1:pos]
	
	key = hashlib.sha512(key + salt).digest()

	clear = crypt(data[pos:], key)
	
	return clear

Računa se od koje pozicije se u podacima nalazi dodani HMAC kako bi se isti mogao usporediti sa ponovno izračunatim HMAC-om te vidjeti da li je došlo do manipulacije sadržajem ili je korišten krivi ključ. Zatim se podaci dekriptiraju te se vraća izvorni tekst. Cijelokupni izvorni kod sa licencom možete vidjeti ovdje: [28].

Još neke opće preporuke vezane uz korištenje stream šifri (ali i drugih):

--Ljubarac 19:45, 19. siječnja 2013. (CET)

WEP protokol

WEP protokol koristi RC4 za stvaranje šifrirane poruke. Izvorni kod cijelog WEP protokola se nalazi ovdje.[[29]] Funkcije koje se koriste za RC4 protokol su opisane u gornjem tekstu. Funkcije koje su potrebne za WEP su slijedeće:
Dodaj IV 

def dodaj_IV(kljuc):
    import random
    import string
    for i in range(3):
        znak = ord(random.choice(string.ascii_letters + string.digits))
        IV.append(znak)
        kljuc.append(znak)
    return kljuc

Ova funkcija uzima ključ nakon što je već obrađen sa algoritmom za prijelaz u brojčane znakove, te generira nasumični ASCII znak, kojeg onda pretvara u brojčanu vrijednost. ASCII znakovno polje je uzeto radi jednostavnosti, funkcija može biti prilagođena da koristi sav raspon mogućnosti 24 bitnog zapisa.
Tako stvoreni IV se zatim dodaje u ključ (na kraju ključa u ovoj imeplementaciji), te se dodaju u polje IV, kojesluži za proslijeđivanje tog vektoru funkciji za dekriptiranje. Time se simulira generiranje istog IV-a od strane routera.
Kriptiraj 

def kriptiraj(kljuc):
    kljuc_kriptiraj = konvertiraj_kljuc(kljuc)
    kljuc_s_IV = dodaj_IV(kljuc_kriptiraj)
    keystream = RC4(kljuc_s_IV)
    for slovo in plaintext:
        cipher.append(ord(slovo) ^ keystream.next())
    return cipher

Ova funkcija uzima ključ, pretvara ga u brojačanu vrijednost pomoću ord funkcije, te mu dodaje IV. Nakon što mu je dodan IV, proslijeđuje tako generiranu listu u RC4 algoritam, koji od koketaniranih IV i ključ polja stvara polje stanja, što je ujedno i ključ za šifriranje poruke.
Šifriranje 

import sys
    for slovo in plaintext:
        cipher.append(ord(slovo) ^ keystream.next())
    return cipher

Ova funkcija uzima poruku i generirani ključ za šifriranje, te ih XOR-a međusobno.
Dekriptiranje 

def dekriptiraj(cipher):
    dekript = []
    kljuc_dekriptiraj = konvertiraj_kljuc(kljuc)
    for znak in IV:
        kljuc_dekriptiraj.append(znak)
    keystream=RC4(kljuc_dekriptiraj)
    procitano = []
    for znak in cipher:
        dekript.append(znak ^ keystream.next())
    for znak in dekript:
        procitano.append(chr(znak))
    return ''.join(procitano)

Ova funkcija ima istu funkcionalnost kao i funkcija kriptiranja, ponovno prolazi kroz RC4 algoritam koristeći ključ (lozinku za wireless pristup) i proslijeđeni IV vektor (na taj način simuliramo generiranje istog IV-a od strane routera).
--Branimir Jurić 23:25, 20. siječnja 2013. (CET)

Sources






Ljubo Barać, Branimir Jurić, Jelena Valčić

Dobavljeno iz "https://security.foi.hr/wiki/index.php/Ispravno_kori%C5%A1tenje_stream_ciphera_nalik_RC4"
Osobni alati
Imenski prostori
Inačice
Radnje
Orijentacija
Traka s alatima