Temu prijavili: Oliver Grbavac, Marko Miletić

Ključni pojmovi

• Diffie-Hellmanov postupak za razmjenu tajnog ključa
• Diffie-Hellmanov protokol s eliptičnom krivuljom

Uvod

Osnovni problem komunikacijskih zaštitnih mehanizama je zaštita poruke i kao najdjelotvornija zaštita poruka je njihovo kriptiranje. Jako je važno, pogotovo u umreženim računalnim sustavima, uspostaviti siguran mehanizam komunikacije. S obzirom da je podatke, u komunikacijskom sustavu, nemoguće zaštititi od prisluškivanja razumnom se pokazalo učiniti podatke nerazumljivima neovlaštenim korisnicima. Još u davnim vremenima Julije Cezar je vrlo često slao tajne poruke koje su bile kriptirane na jednostavan način, ali danas kada imamo moćna računala razlikujemo dva osnovna kriptosustava: simetrični i asimetrični. Današnji kriptosustavi zasnivaju se na postupcima koji se mogu učinkovito izvoditi na računalima, ti se postupci zasnivaju na algoritmima koji su opće poznati, ali s ključevima koji imaju vrlo veliki broj mogućnosti. Upravo to omogućuje stvaranje velikog broja različitih oblika kriptiranog teksta. Asimetrični kriptosustavi imaju različite ključeve kriptiranja i dekriptiranja, dok je dok simetričnih kriptosustava ključ kriptiranja jednak ključu dekriptiranja. Diffie – Hellmanov postupak za razmjenu tajnog ključa koristi asimetrični algoritam. Tvorci ovog algoritma su Whitfield Diffie i Martin Hellman.

Diffie-Hellman postupak za razmjenu tajnog ključa

Diffie i Hellman su 1976. godine objavili svoj postupak za uspostavu simetričnog kriptosustava između dva partnera. Postupak se zasniva na bitnoj različitosti složenosti izračunavanja modularne potencije i izračunavanja diskretnog logaritma. Diffie i Hellman su bili prvi koji su objavili postupak za razmjenu tajnog ključa potrebog za kriptiranje poruka upotrebom simetričnog kriptosustava. Koraci Diffie – Hellman protokola su:

• Dva se sudionika na bilo koji način(npr. objava na internetu) unaprijed dogovore o dva velika broja, n i g. Broj g je relativno prost broj u odnosu na n, a najveći zajednički djeljitelj im je broj 1: nzd(g,n) = 1. Najpraktičnije je za n odabrati veliki prosti broj p. Brojevi p i g ne moraju biti tajni. Oni se mogu javno objaviti.

• Zatim, korisnik 1, neka je to Ana, odabere veliki nasumični prirodni privatni broj x. Korisnik 2, neka je to Ivan, odabere na isti način svoj privatni tajni broj y.

• Ana, koja želi uspostaviti komunikaciju s Ivanom, šalje rezultat izračunavanja operacije modulo: X=g^x (mod p).

• Pero šalje Ani rezultat izračunavanja operacije modulo te u jednadžbi koristi svoj privatni broj y: Y=g^y (mod p).

• Ana zatim izračunava: K = Y^x (mod p) = (g^y)^x (mod p) = g^xy (mod p) . Ana je izračunala ključ koji se može koristiti za kriptiranje poruka.

• Slično, Ivan izračunava: K = X^y (mod p) = (g^x)^y(mod p)= g^xy(mod p).Pero je takođerizračunao ključ kriptiranja koji je jednak onom kojeg je i Ana izračunala.

• Kako su ključevi koje su Ana i Pero izračunali jednaki, oni su upravo razmjenili simetrični ključ kriptiranja.

Izračunata vrijednost K je tajni ključ koji Ana i Ivan mogu koristiti za simetrično kriptiranje. Čak i ako neki napadač prisluškuje komunikaciju između Ane i Ivana te dozna vrijednosti g , p , X ,Y , on ne može izračunati ključ K , osim ako ne uspije izračunati diskretni logaritam od X ili Y . S obzirom da je to vrlo teško, ključ K ostaje tajnim. Dakle, Ana je primjenila svoj privatni ključ x na Ivanovu poruku i izračunala ključ K. Ivan je također primjenio svoj privatni ključ y na Aninu poruku i izračunao ključ K, koji je jednak onom kojeg je izračunala Ana. Na jednostavan način Ana i Ivan sada posjeduju broj koji je poznat samo njima. Sljedeća slika opisuje razmjenu tajnog ključa upotrebom Diffie-Hellmanovog postupka.

Primjer razmjene ključeva upotrebom protokola Diffie-Hellman

Neka se Ana i Ivan dogovore oko brojeva p = 53 i g = 48. Ana odabire svoj privatni broj x = 36 i pošalje Ivanu:

   X = 48^36(mod 53) = 49

Ivan odabire svoj privatni broj i šalje ga Ani:

   Y = 48^40(mod 53) = 44

Nakon toga Ivan i Ana izračunavaju zajednički ključ po sljedećim formulama. Ana ga računa na sljedeći način:

   K = Y^x(mod p) = 44^36(mod 53) = 49,

a Ivan:

   K = X^y(mod p) = 49^40(mod 53) = 49.

Nakon izračuna Ana i Ivan se slažu da je tajni ključ jednak 49. [1]

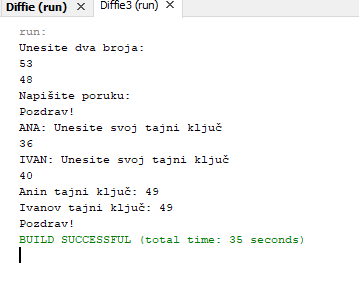
Na sljedećoj slici je prikazan algortima implementiran u programskom jeziku Java.U stvarnosti se koriste mnogo veći brojevi, u implementiranom algoritmu se također mogu koristiti mnogo veći brojevi, ali smo uzeli brojeve iz ranije navedenog primjera.

import java.io.DataInputStream;
import java.math.BigInteger;
import java.util.Scanner;

public class Diffie3 {

   public static void main(String[] args) 
   {
       Scanner stdin = new Scanner(System.in);
       
       BigInteger n, g, x, y, k1, k2, Ana, Ivan;
       String message = "";
       
       System.out.println("Unesite dva broja: ");
       n = new BigInteger(stdin.next());
       g = new BigInteger(stdin.next());
       
       
       System.out.println("Napišite poruku: ");
       message = stdin.next().trim();
       
       System.out.println("ANA: Unesite svoj tajni ključ");
       x = new BigInteger(stdin.next());
       Ana = g.modPow(x, n);
       
       
       System.out.println("IVAN: Unesite svoj tajni ključ");
       y = new BigInteger(stdin.next());
       Ivan = g.modPow(y, n);
       
       k1 = Ivan.modPow(x, n);
       k2 = Ana.modPow(y, n);
       
       System.out.println("Anin tajni ključ: " +k1);
       System.out.println("Ivanov tajni ključ: " +k2);
       
       
       if(k1.equals(k2))
           System.out.println(message);   
       else
           System.out.println("Autenfikacija nije prošla");
           
   }
   

Diffie-Hellmanov protokol s eliptičnom krivuljom

Diffie-Hellmanov postupak razmjene tajnog ključa eliptičnom krivuljom inačica je Diffie-Hellmanovog protokola kojom se dvije osobe mogu dogovoriti oko tajnog ključa koji će se upotrebljavati u daljnjoj komunikaciji.

Kriptografija eliptičnom krivuljom

Kriptografija eliptičnom krivuljom pristup je asimetričnoj kriptografiji koja se temelji na algebarskoj strukturi eliptične krivulje nad konačnim poljima. Kriptografiju eliptičnom krivuljom otkrili su Victor Miller i Neal Koblitz sredinom osamdesetih godina.

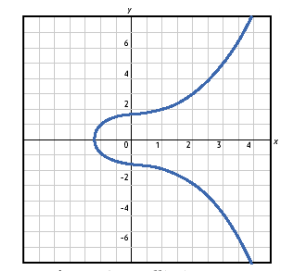
Eliptična krivulja predstavlja skup rješenja (x,y) jednadžbe oblika y^2 = x^3 + ax + b te dodatna točka O koja se zove točka u beskonačnost. U kriptografiji razmatramo konačno polje q elemenata. Ako je q prost broj, polje elemenata su prirodni brojevi dobiveni operacijom modulo q. Pojam polja predstavlja generalizaciju skupa realnih brojeva zajedno s operacijama zbrajanja i množenja realnih brojeva.

Skup točaka na eliptičnoj krivulji čine grupu s određenim pravilom dodavanja, koje se označava simbolom +. Točka O je neutralni element grupe - element koji ne utječe na promjenu rezultata kada se kombinira s ostalim elementima grupe. Kada se u obzir uzima grupa nad konačnim poljem, nužno je da je i grupa konačna.

U kriptografiji s eliptičnom krivuljom, eliptična krivulja se koristi za definiranje elemenata skupa nad kojim se računa grupa, kao i za definiranje operacija među elementima grupe.

Neka postoji graf na čijim se osima nalaze brojevi polja []p, gdje je p prost broj. Ako se definira eliptična krivulja takva da se točke P=(x,y) nalaze na krivulji i zadovoljavaju uvjet da su x i y elementi polja []p, moguće je definirati grupu iz skupa točaka na krivulji. Uz danu točku P i pozitivni prirodni broj n, definira se: [n]P = P + P + ... + P.

Red točke P jednak je najmanjem pozitivnom prirodnom broju n takovom da je [n]P = O. Grupa stvorena nad točkama P označava se sa < P > tj. vrijedi: < P > = {O, P, P + P, P + P + P, ...}

Sigurnost kriptografije eliptičnom krivuljom oslanja se na na problem diskretnog logaritma eliptične krivulje. Neka je E eliptična krivulja nad konačnim poljem []p. Neka je P jedna točka na krivulji E i neka je Q točka u grupi < P >. Potrebno je pronaći broj t takav da vrijedi Q = [t]P. Vrijedi opće uvjerenje da je problem diskretnog logaritma eliptične krivulje računski teško rješiv kada točku P čine veliki prosti brojevi.

Diffie-Hellmanov protokol s eliptičnom krivuljom

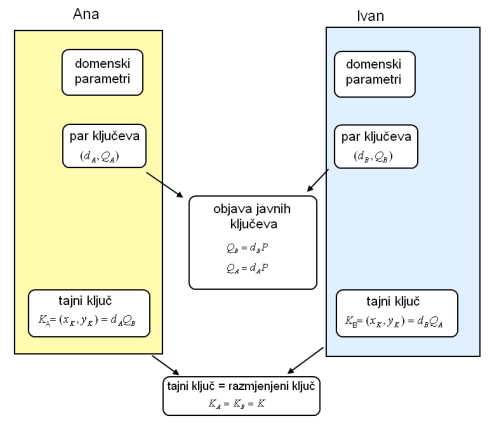
Kada se kriptografija temelji na eliptičnim krivuljama, sve osobe koje žele komunicirati kriptiranim porukama moraju se dogovoriti oko parametara koji definiraju eliptičnu krivulju, tj. o domenskim parametrima. Neka je konačno polje definirano oznakom []p u slučaju da se koriste prosti brojevi. Eliptičnu krivulju definiraju konstante a i b koje se koriste u jednadžbi krivulje. Potrebno je također definirati i cikličku grupu čiji je generator označen sa P. Za primjenu u kriptografiji red generatora P, odnosno najmanjeg nenegativnog broja n takvog da je nP=O, mora biti prost. Kada se koriste prosti brojevi, domenski parametri su (p, a, b, P, n, h), gdje se h naziva kofaktor i to je mali prirodni broj (h < 4) koji se u većini slučajeva postavlja na vrijednost 1. Osim kada postoji uvjerenje da je domenske parametre generirala stranka od povjerenja, domenski se parametri moraju validirati prije upotrebe, što znači potvrditi da su ih generirale osobe koje žele komunicirati. Međutim, uobičajeno je da odabir domenskih parametara ne obavljaju osobe koje žele komunicirati jer proces uključuje prebrojavanje točaka koje se nalaze na eliptičnoj krivulji (što je teško implementirati i zahtjeva mnogo vremena). Zbog toga postoje organizacije koje objavljuju domenske parametre eliptičnih krivulja za polja poznatih veličina kao što su NIST (National Institute of Standards and Technology) i SECG (Standards for Efficient Cryptography Group).

Protokol ćemo objasniti na primjeru komunikacije između dvije osobe. Neka Ana želi razmijeniti tajni ključ s Ivanom, ali jedini komunikacijski kanal koji im je dostupan je javan i postoji mogućnost prisluškivanja. Postupak je sljedeći:

• prvo je potreban dogovor oko domenskih parametara između Ane i Ivana
• Ana i Ivan moraju odabrati par ključeva prikladnih za kriptografiju eliptičnom krivuljom. Par ključeva koji svaki treba odabrati su privatni ključ d, slučajno odabran iz intervala [1, n-1], i javni ključ Q, gdje je Q=dP. Neka par ključeva koje odabire Ana bude (da, Qa) i par ključeva koje odabire Ivan (db, Qb). Ana i Ivan objavljuju svoje javne ključeve.
• Ana računa K = (xk, yk) = daQb i Ivan računa K = (xk, yk) = dbQa, iz čega slijedi da je razmjenjeni ključ K.

Točku K koju Ana i Ivan računaju jednaka je zbog toga što je daQb = dadbP = dbdaP = dbQa.

Protokol je siguran jer su jedini podaci koji su objavljeni javni ključevi i osoba koja prisluškuje ne može otkriti privatni ključ (osim ako ne uspije riješiti problem diskretnog logaritma eliptične krivulje, što nije moguće u realnom vremenu).

Primjer komunikacije dvije osobe koristeći Diffie-Hellmanov protokol s eliptičnim krivuljama

using System;
using System.IO;
using System.Security.Cryptography;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace ECDH
{
   class Program
   {
       static CngKey ivanKey;
       static CngKey anakey;
       static byte[] ivanPubKeyBlob;
       static byte[] anaPubKeyBlob;

       static void Main(string[] args)
       {
           KreirajKljučeve();
           byte[] kripiraniPodaci = IvanSaljePoruku("ultra tajna poruka");
           AnaPrimaPoruku(kripiraniPodaci);
           Console.Read();
       }

       private static void KreirajKljučeve()
       {
           ivanKey = CngKey.Create(CngAlgorithm.ECDiffieHellmanP256);
           anakey = CngKey.Create(CngAlgorithm.ECDiffieHellmanP256);
           ivanPubKeyBlob = ivanKey.Export(CngKeyBlobFormat.EccPublicBlob);
           anaPubKeyBlob = anakey.Export(CngKeyBlobFormat.EccPublicBlob);
       }

       private static byte[] IvanSaljePoruku (string poruka)
       {
           Console.WriteLine("Ivan šalje poruku: {0}", poruka);
           byte[] podaci = Encoding.UTF8.GetBytes(poruka);
           byte[] krpodaci = null;
           using (var ivanAlgoritam = new ECDiffieHellmanCng(ivanKey))
           using (CngKey anaPubKey = CngKey.Import(anaPubKeyBlob, CngKeyBlobFormat.EccPublicBlob))
           {
               byte[] simKljuč = ivanAlgoritam.DeriveKeyMaterial(anaPubKey);
               Console.WriteLine("Ivan kreira simetrični ključ s Aninim javnim ključem: {0}", Convert.ToBase64String(simKljuč));
               using (var aes = new AesCryptoServiceProvider())
               {
                   aes.Key = simKljuč;
                   aes.GenerateIV();
                   using (ICryptoTransform encryptor = aes.CreateEncryptor())
                   using (MemoryStream ms = new MemoryStream())
                   {
                       var cs = new CryptoStream(ms, encryptor, CryptoStreamMode.Write);
                       ms.Write(aes.IV, 0, aes.IV.Length);
                       cs.Write(podaci, 0, podaci.Length);
                       cs.Close();
                       krpodaci = ms.ToArray();
                   }
                   aes.Clear();
               }
           }
           Console.WriteLine("Ivan: Poruka je kriptirana: {0}", Convert.ToBase64String(krpodaci));
           Console.WriteLine();
           return krpodaci;
       }

       private static void AnaPrimaPoruku(byte[] kriptiraniPodaci)
       {
           Console.WriteLine("Ana prima kriptiranu poruku");
           byte[] podaci = null;
           var aes = new AesCryptoServiceProvider();
           int nBytes = aes.BlockSize >> 3;
           byte[] iv = new byte[nBytes];
           for (int i = 0; i < iv.Length; i++) iv[i] = kriptiraniPodaci[i];
           using (var anaAlgoritam = new ECDiffieHellmanCng(anakey))
           using (CngKey ivanPubKey = CngKey.Import(ivanPubKeyBlob, CngKeyBlobFormat.EccPublicBlob))
           {
               byte[] simKljuč = anaAlgoritam.DeriveKeyMaterial(ivanPubKey);
               Console.WriteLine("Ana kreira simetrični ključ s Ivanovim javnim ključem: {0}", Convert.ToBase64String(simKljuč));
               aes.Key = simKljuč;
               aes.IV = iv;
               using (ICryptoTransform decryptor = aes.CreateDecryptor())
               using (MemoryStream ms = new MemoryStream())
               {
                   var cs = new CryptoStream(ms, decryptor, CryptoStreamMode.Write);
                   cs.Write(kriptiraniPodaci, nBytes, kriptiraniPodaci.Length - nBytes);
                   cs.Close();
                   podaci = ms.ToArray();
                   Console.WriteLine("Ana dekriptira poruku: {0}", Encoding.UTF8.GetString(podaci));
               }
               aes.Clear();
           }
       }
   }
}

Primjena Diffie-Hellmanovog protokola

Diffie-Hellmanov protokol je postupak koji osigurava razmjenu tajnog ključa kriptiranja putem nezaštićenog komunikacijskog kanala. Kao takav, koristi se u mrežnim protokolima koji omogućuju zaštićenu komunikaciju:

• kod autentifikacije u mrežama računala
• u IPsec (IP security) protokolu
• unutar IKE (Internet Key Exchange) strukture
• SSH i TLS protokolima
• u postupku stvaranja digitalnih potpisa i digitalnih certifikata

Literatura

1. Diffie-Hellman protokol, dostupno na http://www.cert.hr/sites/default/files/NCERT-PUBDOC-2009-12-284.pdf

2. NIST, dostupno na https://www.nist.gov/

3. SECG, dostupno na http://www.secg.org/

4. Korištenje eliptičnih krivulja u kripotografiji, dostupno na https://www.cis.hr/www.edicija/LinkedDocuments/CCERT-PUBDOC-2006-11-169.pdf

5. Diffie - Hellman Key Exchange, dostupno na https://www.youtube.com/watch?v=cM4mNVUBtHk&t=34s