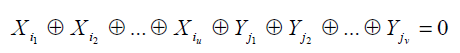Iva Kiš, Nikola Pavetić, Jurica Sugnetić, Anita Završki, Antonio Zrinušić

Sadržaj 1 Kriptiranje 1.1 Kriptiranje i kodiranje 1.2 Povijest kriptografije 1.3 Najpoznatiji načini kriptiranja kroz povijest 1.3.1 Hijeroglifi 1.3.2 Hebrejska šifra 1.3.3 Skital 1.3.4 Cezarova šifra 1.3.5 Polybiusov kvadrat 1.4 Povijest moderne kriptografije 2 Simetrična kriptografija 2.1 DES algoritam (Data Encryption Standard) 2.1.1 Kako radi DES? 2.2 IDEA algoritam (International Data Encryption Algorithm) 2.3 AES algoritam (Advanced Encryption Standard) 3 Kriptoanaliza 3.1 Povijest kriptoanalize 3.2 Klasična kriptoanaliza 3.3 Moderna kriptoanaliza 4 Linearna kriptoanaliza 4.1 Povijest linearne kriptoanalize 4.2 Općenito o linearnoj kriptoanalizi 4.3 Matematička pozadina linearne kriptoanalize 4.3.1 Jednostavna supstitucijsko-permutacijska mreža 4.4 Pregled osnovnog napada linearne kriptoanalize 4.5 Linearna kriptoanaliza kriptosustava kriptiranog jednostavnom zamjenom (eng. toy cipher) 4.6 Primjer linearne kriptoanalize (S-DES) 4.7 Linearni napad 4.7.1 Linearni napad na DES (4 runde) 5 Literatura 6 Doprinosi

Kriptiranje

Riječ kriptografija dolazi od grčkih riječi kriptos što znači skriveno i grafos što znači pisati. Stoga bi riječ mogli doslovno prevesti kao „skriveno pisanje“. Kriptografija se koristila još u antičkoj Grčkoj. Naprava zvana skital bila je drveni štap oko kojeg se namotala vrpca, a na nju se okomito pisala poruka. Zatim bi se vrpca odmotala i poruku bi mogao pročitati samo onaj koji je imao štap jednake debljine. Od samih početaka kriptografije, koju je već na neki način i Cezar definirao, ona se razvila u složenu matematičku disciplinu. Kriptografija nam omogućuje osiguravanje svih sigurnosnih zahtjeva osim raspoloživosti. Prema nekim autorima, prve naznake kriptiranja pronalaze se u starom Egiptu i Indiji već 3000 godina prije Krista, ali to su bili malo drugačiji načini. Naime, stvoren je novi jezik koji je bio poznat samo jako malom broju ljudi te su se na taj način prenosile poruke. Počevši od Cezara pa preko skriptala kriptografija je dobila smisao onakav, kakav ga mi danas vidimo. Kriptografija je znanstvena disciplina koja se bavi proučavanjem metoda za slanje poruka u takvom obliku da ih samo onaj kome su namijenjene može pročitati. [Prema 7]

Izvor: slika

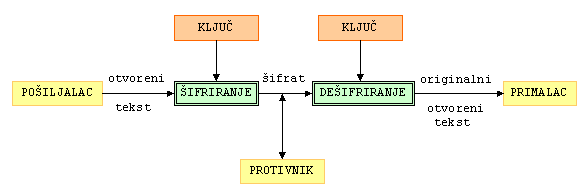
Osnovni zadatak kriptografije jest omogućiti dvjema osobama - pošiljatelju i primatelju (u literaturi su često upotrebljavana imena Alice i Bob) komuniciranje preko nesigurnog komunikacijskog kanala (telefonska linija, računalna mreža, ...) na način da treća osoba, njihov protivnik (u literaturi se najčešće zovu Eva ili Oskar), koja može nadzirati komunikacijski kanal, ne može razumjeti njihove poruke. Poruku koju pošiljatelj želi poslati primatelju zvat ćemo otvoreni tekst. To može biti tekst na njihovom materinjem jeziku, numerički podaci ili bilo što drugo. Pošiljatelj transformira otvoreni tekst koristeći unaprijed dogovoreni ključ. Taj postupak se naziva šifriranje, a dobiveni rezultat šifrat ili kriptogram. Nakon toga pošiljatelj šalje šifrat preko nekog komunikacijskog kanala. Protivnik prisluškujući može doznati sadržaj šifrata, ali ne može odrediti otvoreni tekst. Za razliku od njega, primatelj koji zna ključ kojim je šifrirana poruka može dešifrirati šifrat i odrediti otvoreni tekst. [Prema 7]

Izvor: 7

 

Kriptiranje i kodiranje

Česta greška je poistovjećivanje pojma kriptiranje i kodiranje. Zbog toga će se u ovom kratkom poglavlju pokušati objasniti razlika između ta dva pojma. Postavlja se pitanje: "Što je zapravo kodiranje, a što kriptiranje?" Kriptiranje (eng. encryption) je proces pretvaranja informacije u nečitljiv oblik svakome, osim onima koji posjeduju specifični kriptografski ključ. Kodiranje (eng. encoding) je pretvaranje poruke u simbole, kao što je pretvaranje govornog jezika u pisani jezik ili fizičkih zakona u matematičke simbole.

Ove dvije definicije dosta su slične, međutim velika je razlika između ta dva pojma. Jednostavno, kriptiranje je nešto kao pravljenje tajne poruke tako da mijenjamo ili premještamo znakove prema prije definiranom pravilu. Pravilo možemo zvati ključ, a sam format poruke se nije promijenio. Kad kodiramo, format podataka se mijenja. Na primjer kad snimamo zvuk, mikrofon će kodirati analogni signal u digitalni signal i tada taj signal možemo spremiti, čime se format promijenio. Kodirani podatak nije nužno tajan kao što je to slučaj kod kriptiranja. [Prema 8]

Povijest kriptografije

Kao što je već napomenuto, kriptografija postoji još od antičkih vremena. Poznato je da su čak Egipćani, prije više od 4000 godina, koristili primitivne šifarske sisteme. Osnovu skoro svih algoritama čine matematički postupci supstitucije (zamjene) i transpozicije (permutacije). Supstitucija znači zamjena nekog dijela jasnog teksta s nekim drugim znakovima ili rezultatom funkcije čiji su ulaz ti znakovi i ključ. Permutacija pak znači da se originalna poruka preuredi po nekom algoritmu. Šifriranje supstitucijom obuhvaća:

1. monoalfabetsku zamjenu – bijektivno preslikavanje, tj. svaki znak poruke se preslikava u točno jedan znak šifrirane poruke;
2. polialfabetsku zamjenu – preslikavanje 1-n, tj. svaki znak poruke može se preslikati u jedan od n dozvoljenih znakova šifrirane poruke, ovisno o algoritmu i dužini ključa koji se koriste;
3. poligramsku zamjenu – bijektivno preslikavanje pri kojem se kao osnovna jedinica supstitucije uzima poligram (niz od više znakova).

Najpoznatiji načini kriptiranja kroz povijest

Hijeroglifi

Stari Egipćani počeli su koristiti Hijeroglife oko 2000 godina prije Krista. Hijeroglifi su zapravo male sličice stvari i pojava koje prikazuju i opisuju život te veličaju uspjeh faraona. Problem je bio u tome što je ista sličica predstavljala različite pojmove. Njima su ukrašavane grobnice te prvobitno nisu bili izmišljeni u svrhu skrivanja teksta, već da ih manji broj ljudi zna pročitati. Hijeroglifi su proučavani dugi niz godina, a francuski arheolog J. F. Champollion uspio ih je dešifrirati. Za razumijevanje tekstova hijeroglifa potrebne su goleme jezično-komparativne studije zasnovane na srodnosti kopskog jezika sa starim egipatskim jezikom. [Prema 9]

Hebrejska šifra

Stara Mezopotamija koristila je sličnu metodu kriptiranja kao i Egipat. Oni su koristili tzv. klinasto pismo. Hebrejska šifra se zasnovala na principu zamjene slova abecede. Najpoznatija hebrejska šifra je poznata pod nazivom atbash. Kada bi klinasto pismo preveli na slova engleske abecede, tablica šifrata bi izgledala:

A B C D E F G H I J K L M Z Y X W V U T S R Q P O N

što znači da se slovo A mijenja sa slovom Z i obrnuto. Poznate su još šifrati albam i atban. Kod njih je drugačiji šifrat, ali princip je isti. [Prema 9]

Skital

Kriptografija se kao sredstvo komuniciranja pojavila u Grčkoj, odnosno Spartanci su 400 godina prije Krista počeli koristiti kriptirane poruke. Skital je bio drveni štap oko kojeg se namotao tanki list papirusa, a na njega se okomito pisala poruka. Zatim bi se vrpca odmotala i poruku bi mogao pročitati samo onaj koji je imao štap jednake debljine. Slika skitala je prikazana na vrhu stranice.

Cezarova šifra

Cezarova šifra dobila je naziv po vojskovođi i rimskom vladaru Juliju Cezaru. Bila je to jednostavna kriptirana poruka koja je kao šifrat koristila posmak cijele abecede za dva mjesta ulijevo. Koristila se oko pedesetih godina prije Krista. [Prema 9]

ABCDEFGHIJKLMNOPQRSTUVWXYZ CDEFGHIJKLMNOPQRSTUVWXYZAB

Polybiusov kvadrat

Slova abecede postavljaju se u kvadrat 5x5 te se redovi i stupci numeriraju od 1 do 5, tako da svako slovo predstavlja odgovarajući par retka i stupca. Dekriptiranje se obavlja pridruživanjem svakom od parova odgovarajuće slovo abecede.

Od samih početaka pa do danas prošlo je puno vremena, kroz cijeli srednji vijek, a i kasnije, kriptiranje je sve više i više unaprjeđivano. Laganim koracima došlo se do onoga što danas poznajemo. Jedno vrijeme, uobičajeni način slanja poruka između vojskovođa, visokih državnih dužnosnika, bilo je upravo kriptiranje. Stoga su se često razvijale nove ideje i novi načini kako bi se poruke čim bolje zaštitile. [Prema 9]

Tako bi se primjerice kratica SIS mogla zapisati kao 44 42 44.  

Povijest moderne kriptografije

Kriptografija je imala izuzetno važan utjecaj tijekom cijelog dvadesetog stoljeća. Tridesetih godina prošlog stoljeća vlada Sjedinjenih Američkih Država zanemarila je kriptoanalizu. Poznata je rečenica tajnika Henrya L. Stimsona kojom je komentirao potez ukidanja aktivnosti na razvijanju kriptoanalize: „Gospoda ne čitaju tuđu poštu.“ Nakon što je SAD pretrpio napad na Pearl Harbor, 07.12.1941. godine, ubrzo su ponovno počele aktivnosti na polju kriptoanalize jer je prijašnje zanemarivanje imalo velik učinak na ogromne žrtve pretrpljene iznenadnim napadom Japanaca na vojnu bazu. Kasnije je kriptoanaliza saveznika bila toliko razvijena da su probijeni gotovo svi kriptosustavi Sila osovine što ima veliku važnost i za konačan ishod rata koji je obilježio stoljeće. Postoje brojni primjeri važnosti pojedinih kriptosustava i kriptoanaliza iz Drugog svjetskog rata (npr. stroj za kriptiranje Enigma), no razdoblje nakon Drugog svjetskog rata je vrijeme kada se kriptografija počinje promatrati i proučavati, ne kao ratno oružje, već u pravom svijetlu znanosti, da mora služiti u humane svrhe. Razvojem računala sedamdesetih godina prošlog stoljeća, kriptografijom se ne bave samo vladine organizacije, već i ostale organizacije zbog potrebe zaštite ogromne količine digitalnih podataka. Tako prvi standardni kriptosustav postaje DES (eng. Data Encryption Standard). DES otvara mnoga vrata, znanstvenici se počinju globalno baviti kriptografijom, razvijaju se novi kriptosustavi pa se otkrivaju i asimetrični kriptografski algoritmi. [Prema 1]

Simetrična kriptografija

Linearna kriptoanaliza usko je vezana uz simetričnu kriptografiju pa je za potrebe boljeg razumijevanja kriptoanalize potrebno objasniti i simetričnu kriptografiju. Za nju je karakteristično da za kriptiranje i dekriptiranje poruke mora postojati identičan ključ. Gledajući povijesni pregled, primjerice, u slučaju skitala bi za čitanje poruke primatelj morao biti drveni štap jednake debljine kao pošiljateljev. Iako se kriptografija razvijala, i dalje je za kriptiranje i dekriptiranje poruke bilo potrebno imati identični ključ pa se uvijek javljala opasnost da poruku pročita bilo tko ukoliko ima ključ. Prilikom razmjene ključeva, važno je da se razmjena odvije u tajnosti.

Komunikacijski kanal za razmjenu kriptografskih ključeva u izvornom obliku mora biti siguran, tj. mora onemogućiti trećoj strani da sazna bilo kakvu informaciju o ključevima. U suprotnom, kriptiranje poruka kompromitiranim ključevima rezultiralo bi kompromitiranjem štićenih podataka i ne bi imalo nikakvog smisla. Uobičajeno je da se kod simetričnih kriptografskih sustava potrebni kriptografski ključevi unaprijed razmjene između korisnika. [12]

Prikaz procesa simetrične enkripcije [13]

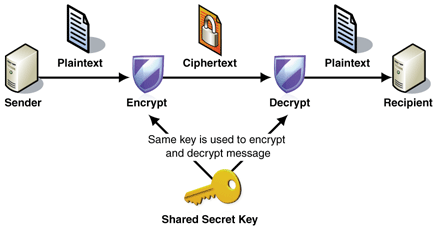
Sa slike je vidljivo da pošiljatelj (Sender) šalje kriptirani dokument (Ciphertext) tako što je izvršio enkripciju poruke (Plaintext) pomoću nekog od algoritama simetrične enkripcije i tajnog ključa. Primatelj poruke (Recipient) je primio kriptirani tekst, a kako bi ga uspio pročitati, prvo mora izvršiti dekripciju pomoću tajnog ključa. Pretpostavlja se da oba sudionika razmjene poruka imaju identični tajni ključ.

Općenito, radi postojanja samo jednog tajnog ključa, algoritmi simetrične kriptografije su obično brzi i upotrebljavaju se za šifriranje velikih količina podataka. Osim toga, relativno je jeftino kreirati snažan ključ za ovakvo kriptiranje jer ključevi imaju tendenciju biti puno manji u odnosu na razinu zaštite koju mogu pružiti i ove algoritme je relativno jeftino izraditi i implementirati. Stoga, ova vrsta kriptografije može biti vrlo učinkovita. Osim brze enkripcije i dekripcije podataka, simetrična kriptografija pruža određeni stupanj autentičnosti. Naime, proces autentikacije se može izvršiti jer se poruka može pročitati samo s tim jednim tajnim ključem i nijednim drugim pa druga strana može biti sigurna da komunicira s dobrom stranom dok god može dešifrirati poruke i dotle one imaju smisla. No, to funkcionira samo ako je simetrični ključ stvarno tajna između dvije strane, odnosno da nema drugih strana koje znaju taj isti ključ. Ako je ključ, slučajno ili namjerno, otkriven, to utječe na povjerljivost i sigurnost poslanih poruka. Prema tome, nedostatak jest upotreba jednog tajnog ključa kojeg moraju imati obje strane: i pošiljatelj i primatelj poruke. Problem razmjene ključeva rješava se tako da se obje strane osobno sretnu i razmjene ključeve (no tu se javlja pitanje da, ako su se već susreli da razmjene ključeve, zašto nisu odmah i razmijenili poruke) ili upotrebom drugih sustava kriptiranja kao što su algoritmi asimetričnog kriptiranja. Sve u svemu, simetrična kriptografija igra važnu ulogu u SSL protokolu te enkripciji preko TCP/IP mreže. [prema 14]

Neki od algoritama simetrične kriptografije su DES algoritam, IDEA algoritam i AES algoritam te će u nastavku biti objašnjeni.

DES algoritam (Data Encryption Standard)

DES je skraćenica od Data Encryption Standard. DES je proglašen standardom za kriptiranje 1976. godine, te je od onda tu titulu zadržao sve do 2001. godine koju tada preuzima AES. On radi na principu da kriptira grupe podataka veličine 64 bita. No, u DES-u se svaki osmi bit ključa ignorira, te je zbog toga duljina ključa 56 bita. Tokom razvijanja DES-a NSA (National Security Agency) je pokušala nagovoriti IBM (koji je razvijao DES) da veličina ključa bude 48 bita. IBM je zahtijevao 64 bitni ključ. Na kraju su se našli, možemo reći na pola puta, te je ključ koji koristi DES veličine 56 bita.

Spomenuli smo da DES algoritam radi sa podacima veličine 64 bita. Odnosno on kriptira grupe podataka od kojih je svaki veličine 64 bita. Tako na primjer možemo sljedeći tekst: "8787878787878787". Ukoliko taj tekst kriptiramo sa tajnim DES ključem: "0E329232EA6D0D73", dobivamo sljedeći rezultat: "0000000000000000", što je u biti kriptirani tekst. Isto tako, naravno ukoliko kriptirani tekst ponovno provedemo kroz DES, samo obrnutim postupkom, znači dekriptiramo ga, dobit ćemo početni tekst. U ovom slučaju niz od 16 brojeva gdje se ponavljaju brojevi 8 i 7. No ovdje možemo primijetiti da je u pitanju točno 16 znakova teksta kojeg je potrebno kriptirati. To znači točno 64 bita, točno onoliko koliko je potrebno DES algoritmu za kriptiranje. Sada se postavlja pitanje što kada se DES algoritmu na kriptiranje da tekst koji nije djeljiv sa 64, odnosno zadnji dio neće imati 64 bita koliko mu je potrebno za kriptiranje. Kao primjer ćemo uzeti englesku rečenicu: "Your lips are smoother than vaseline". Ona se sastoji od 36 znakova. Ukoliko to pretvorimo u heksadecimalno, dobivamo 72 znaka. No u bitovima to iznosi 144. Kao što možemo vidjeti, 144 nije djeljivo sa 64 bez ostatka. Kao rješenje dijeljenja dobivamo 2.25. Ovih 0.25 označava zadnjih 16 bitova. Što s tim? Tih zadnjih 16 bitova moramo "nadograditi" do 64 bita, kako bi se uspješno mogao sprovesti DES algoritam. Kada se rečenica pretvori u heksadecimalni zapis, na njezin kraj se dodaje "0D0A" što označava kraj dokumenta, odnosno u ovom slučaju teksta. Nakon toga dopišu se nule, onoliko koliko ih je potrebno. Poruka se zatim normalno kriptira DES algoritmom, budući da sada sadržava blokove po 64 bita koliko je DES-u potrebno.[Prema 22]

Kako radi DES?

Princip rada DES-a ćemo pokazati na primjeru. Poruku ćemo označiti sa M, i ona neka bude:

M = "0123456789ABCDEF". To je zapis u heksadecimalnom formatu.

M = "0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111"

Ovdje vidimo poruku zapisanu u binarnom formatu. Ona se dijeli na dva djela. Na lijevi i desni. Od tih dijelova, svaki je jednake duljine. Prvu polovicu ćemo označiti sa L, a drugu sa D.

L = "0000 0001 0010 0011 0100 0101 0110 0111"

D = "1000 1001 1010 1011 1100 1101 1110 1111"

Kao što smo već ranije rekli DES algoritam koristi 56 bitni ključ. U biti je on 64 bitni, no svaki 8 bit ključa se ne koristi. Ovdje ćemo ključ označiti sa K.

K = "133457799BBCDFF1" u heksadecimalnom zapisu i 

K = "00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001" u binarnom zapisu.

Ključ se sada permutira prema sljedećoj tablici PC-1:

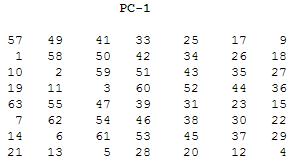
U tablici vidimo brojeve od 1 do 64. Što nam oni znače? Oni označavaju na koji način se dobije permutirani ključ. Vidimo da je tablica dimenzija 7 x 8. Tako da kada originalni ključ provedemo kroz ovu tablicu na izlazu ćemo dobiti 56 bitova, što je u biti veličina ključa koju DES algoritam i koristi. Primjerice 57 bit ključa K će sada postati prvi bit, zatim 49 bit ključa će postati drugi bit ključa, 12 bit ključa će sad postati predzadnji i 4 bit ključa će postati zadnji bit. Slijedi ključ koji smo dobili nakon izvršene permutacije:

Kp = "1111000 0110011 0010101 0101111 0101010 1011001 1001111 0001111".

Sada se ključ također kao i tekst dijeli na dvije polovice:

KL = "1111000 0110011 0010101 0101111"

KD = "0101010 1011001 1001111 0001111"

Kako DES algoritam koristi 16 pod ključeva, oni se sada kreiraju iz KL i KD prema sljedećoj tablici.

Tablica ima 16 ponavljanja. U svakoj iteraciji dobiva se jedan novi pod ključ. Sistem kako nastaje novi pod ključ je prikazan tablicom te ćemo ga sada malo detaljnije objasniti. U prvoj iteraciji nastaje prvi pod ključ tako da se u KL i KD svaki bit pomakne za jedan bit ulijevo. U sljedećoj iteraciji ne uzimamo više KL i KD, nego novo nastale KL1 i KD2 (prvi pod ključ). Tako drugi ključ dobivamo ponovno jednim pomakom ulijevo svih bitova prvog pod ključa. Ova radnja se ponavlja za svaku iteraciju, jedino je razlika u tome da se u pojedinim iteracijama radi pomak za 2 ulijevo. Krajnji rezultat je da dobijemo 16 pod ključeva.

Nakon što smo dobili svih 16 pod ključeva dolazimo do još jedne tablice zamjene.

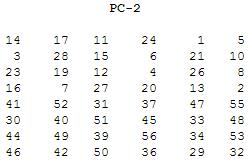
Ovdje je tablica dimenzija 6x8 što znači da ćemo od 56 bitova svakog pod ključa na kraju imati samo 48 bitova koji se u stvari koriste. Tablica funkcionira na istom principu kao i prethodna pa ju nećemo još jednom objašnjavati. Prema toj tablici se permutira svih 16 pod ključeva.

Sada dolazimo do poruke. Kako imamo tablice permutacije za ključeve i pod ključeve, tako imamo i jednu tablicu permutacije za poruke. Poruka, tekst koji treba kriptirati se rastavi na blokove od 64 bita, što smo ranije već objasnili kako, te se zatim svaki od tih blokova permutira prema sljedećoj tablici.

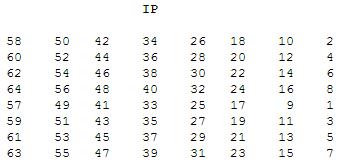
Tablica je dimenzija 8x8 što odgovara veličini bloka od 64 bita, te ovaj put ne gubimo niti jedan bit, kao što je to bio slučaj u prethodne dvije permutacije. Tekst M sa početka se sada permutira prema toj tablici i dobijemo sljedeći permutirani tekst.

MP = "1100 1100 0000 0000 1100 1100 1111 1111 1111 0000 1010 1010 1111 0000 1010 1010"

Nakon permutacije tekst se dijeli na pola:

MPL = "1100 1100 0000 0000 1100 1100 1111 1111"

MPD = "1111 0000 1010 1010 1111 0000 1010 1010"

Sada dolazimo do dijela koji se ponavlja 16 puta, odnosno možemo to reći rundi. Ovo će nam biti potrebno, no linearnu kriptoanalizu ćemo pokazati na primjeru sa samo 3 runde, odnosno 3 ponavljanja. Kako bi što lakše shvatili ovaj dio ponovno ćemo zapisati neke elemente koje smo vidjeli ranije a koji su nam sada potrebni.

K1 = "000110 110000 001011 101111 111111 000111 000001 110010"

L0 = MPL = "1100 1100 0000 0000 1100 1100 1111 1111"

R0 = MPD = "1111 0000 1010 1010 1111 0000 1010 1010"

Slijede dvije jednadžbe koje će se sada izvesti nad ovim podacima. Preimenovali smo tekst u L0 i R0 kako bi lakše shvatili što se događa i koristi u iteracijama. Teško bi bilo pratiti da smo ostavili MPD i MPL.

Ln = Rn-1

Rn = Ln-1 + f(Rn-1,Kn)

Taj dio se ponavlja 16 puta. Za n=1 imamo:

K1 = "000110 110000 001011 101111 111111 000111 000001 110010"

L1 = R0 = "1111 0000 1010 1010 1111 0000 1010 1010"

R1 = L0 + f(R0,K1)

Jedini nejasni dio ovdje je još funkcija f i kako ona radi. Kako bi ju mogli izračunati trebamo od R0 koji sadrži 32 bita dobiti 48 bita podataka. To se radi prema tablici selekcije u kojoj se neki bitovi ponavljaju. Slijedi tablica.

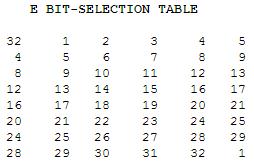
Prema toj tablici mi iz R0 dobijemo:

R0E = "011110 100001 010101 010101 011110 100001 010101 010101"

Sljedeći korak u funkciji f je XOR R0E sa pod ključem K1. Tim korakom je završilo računanje funkcije f. Ovdje sada slijedi dio koji će nam biti najzanimljiviji budući da ćemo njega kasnije trebati kod linearne kriptoanalize. Nakon XOR operacije smo dobili sljedeće:

f(R0,K1) = "011000 010001 011110 111010 100001 100110 010100 100111".

Ovdje možemo vidjeti grupe po 6 bitova. Ukupno 8 takvih grupa. Svaka od tih 6 grupa će nam sada dati adresu za različitu S kutiju. Pojam S kutije ćemo objasniti kasnije. Adresa koju će nam određena grupa dati će biti 4 bitni broj, koji će zatim zamijeniti sadašnji 6 bitni. To će se napraviti za svaku grupu, te ćemo na kraju kao rezultat od početnih 48 bitova dobiti broj od 32 bita. Ukoliko ste pažljivo pratili, sada ponovno imamo 32 bitni podatak, koji smo imali i prije cijele ove transformacije i funkcije, no u potpunosti izmijenjen. Sada ćemo prikazati S kutiju za prvu grupu.

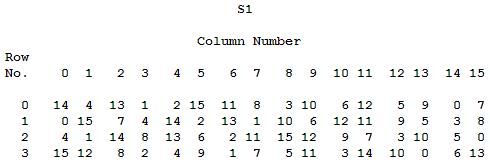
S1 kutija sadrži 4 reda i 16 stupaca. Oni nam govore koji broj će nakon što ga pronađemo u S1 kutiji biti izlaz iz kutije. Ulaz u ovu tablicu je prva grupa od 6 bitova, dok će izlaz biti 4 bita. Kako sad to? Prvi i zadnji bit ulaza kada ih pretvorimo iz binarnog zapisa u dekadski će nam dati indeks retka, dok će ostala četiri bita dati indeks stupca. Element na toj poziciji je izlaz iz S1 tablice i rješenje koje dalje koristimo. Slijedi opis za prvu grupu.

G1 = "011000"

Prvi i zadnji bit su 0 i 0. Binarni broj 00 je dekadski broj 0.Prema tome indeks retka rješenja je 0. Ostala 4 bita su 1100 što u binarnom predstavlja broj 12. Iz toga znamo da će stupac koji gledamo biti na indeksu broj 12. Kada pogledamo redak 0 i stupac 12, dolazimo do elementa koji je 5. To je rješenje i izlaz iz S1 tablice. Naravno, moramo ga zapisati u binarnom obliku.

S1(G1) = "0101"

Ovdje je pokazano samo za prvu grupu, no taj postupak se izvodi za svih osam grupa, te svaka od tih osam grupa ima različitu S kutiju. Krajnje rješenje našeg broja glasi:

S( f(R0,K1)) = "0101 1100 1000 0010 1011 0101 1001 0111"

Kao zadnji korak funkcije f ostaje nam permutacija izlaza iz S kutija, kako bi dobili krajnju vrijednost funkcije f. Permutacija se vrši prema sljedećoj tablici.

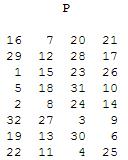
Kako već imamo opisanu permutaciju, stavit ćemo konačno rješenje.

P = "0010 0011 0100 1010 1010 1001 1011 1011"

Ovo do sada opisano je jedna runda, odnosno jedno ponavljanje u DES algoritmu. Na isti način se izvodi svih 16 ponavljanja ili rundi. Na kraju svih ponavljanja imamo zadnju permutaciju koja se izvodi prema sljedećoj tablici.

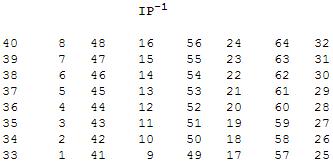
Nakon svih izvedenih 16 rundi i izvršene zadnje permutacije prema ovoj tablici dobivamo tekst koji je kriptiran DES algoritmom. Da se podsjetimo. Naš ulazni tekst je bio:

M = "0123456789ABCDEF"

Dok je rezultat algoritma, odnosno kriptirani tekst:

C = "85E813540F0AB405".[Prema 22]

IDEA algoritam (International Data Encryption Algorithm)

[prema 15, 16, 17]

Algoritam je prvi puta opisan 1991. godine, a opisali su ga J. Massey (ETH Zurich) i Xuejia Lai (Shanghai Jiao Tong University) kako bi zamijenio DES algoritam, a u konačnoj verziji se pojavio 1992. godine. Također se koristi kao opcionalni algoritam u OpenPGP standardu. Najpoznatija primjena ovog algoritma je u PGP paketu koji je prvenstveno namijenjen autentikaciji i kriptiranju e-mailova, a osim toga može poslužiti za zaštitu podataka u datotekama, diskova i slično.

Algoritam se bazira na impresivnim teorijskim temeljima pa se pokazuje kao vrlo otporan na sve vrste napada. Stručnjaci procjenjuju da je jedan od najsigurnijih simetričnih algoritama koji se danas koriste. Trenutno je, u komercijalnoj primjeni, DES još uvijek vodeći algoritam po korištenju, djelomično i zato jer je IDEA bila patentirana do 2012. te je za komercijalnu upotrebu potrebna odgovarajuća licenca. Prilikom razvoja algoritma nije bilo miješanja nekih državnih institucija pa se ne sumnja u postojanje bilo kakvog backdoora, za razliku od DES-a, u čijem je razvoju određeni utjecaj imala i NSA.

Osnova algoritma su tri operacije: logička operacija ekskluzivno ili (XOR), zbrajanje modulo 2¹⁶ (65.536) i multiplikacija modulo 2¹⁶+1 (65.537). Svaku od tih operacija jednostavno je implementirati sklopovski ili programski, što ubrzava sam postupak šifriranja/dešifriranja. Algoritam se sastoji od 8 koraka koji su funkcijski identični. U svakom koraku kao ulaz se koriste četiri 16-bitna bloka koji su generirani u prethodnom koraku, dok su rezultat funkcije koja se provodi u svakom koraku također četiri 16-bitna izlazna bloka.

Prikaz rada IDEA algoritma

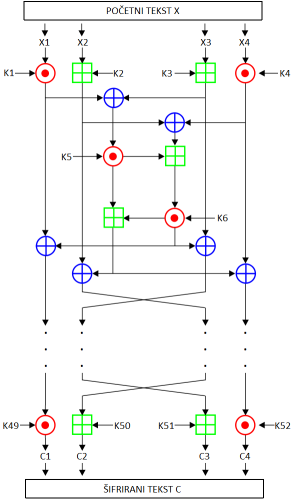
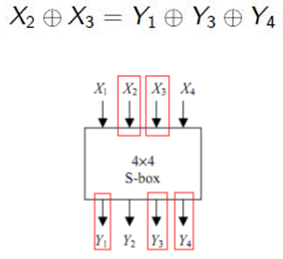
IDEA kriptira poruku u 64-bitnim blokovima i to tako da se blok podijeli na četiri 16-bitna podbloka (X₁, X₂, X₃, X₄) koji predstavljaju ulazne parametre prvog od osam koraka algoritma. Ključ za kriptiranje je duljine 128 bita te se od njega generiraju ukupno pedeset i dva 16-bitna podključa (K₁ … K₅₂) tako da se ključ dijeli na osam 16-bitnih ključeva koji se koriste kao podključevi za prvu iteraciju i prva dva ključa druge iteracije jer se tijekom svake iteracije koristi šest podključeva. Zatim se ključ rotira 25 bitova ulijevo pa se generira sljedećih osam ključeva koji se koriste kao preostala četiri podključa druge iteracije i četiri podključa treće iteracije itd. U svakom od koraka na podblokovima se izvodi XOR operacija (na slici označeno plavo), zatim modulo zbrajanje (na slici označeno zeleno) te na kraju modulo multiplikacija (na slici označeno crveno) međusobno i sa šest 16-bitnih podključeva: dva su korištena tijekom koraka, a četiri se koriste između dva koraka. Između svakog od koraka algoritma drugi i treći podblok se zamjenjuju. Konačno, četiri podbloka se kombiniraju sa četiri podključa dajući tako konačnu transformaciju.

Algoritam za dešifriranje je potpuno identičan, osim što se podključevi generiraju na malo drugačiji način. Podključevi koji se koriste za dešifriranje primjenjuju se obrnutim redoslijedom te su aditivno ili multiplikativno inverzni ključevima za šifriranje.

Što se tiče sigurnosti, algoritam je zasad prilično siguran, no daljnjim razvojem matematičkih metoda i operacija, uvijek postoji mogućnost probijanja algoritma. Jedini nedostatak koji je dosad pronađen su određeni ključevi. Naime, ukoliko se koristi jedan od ključeva oblika:

 0000, 0000, 0x000, 0000, 0000, 000x, xxxx, 0x000

gdje je "x" bilo koji heksadecimalni broj, moguće je takav ključ identificirati kroz napad korištenjem odabranog otvorenog teksta (eng. chosen plaintext attack). Ukoliko se koristi generator pseudoslučajnih brojeva, vjerojatnost pojavljivanja ovakvog ključa je vrlo mala (1/2⁹⁶). Ako se želi eliminirati i ta mala mogućnost, tada je potrebno za svaki podključ izvesti XOR operaciju s vrijednosti 0x0DAE. Po potrebi, sigurnost IDEA algoritma može se povećati upotrebom dodatnih modifikacija tog algoritma.

AES algoritam (Advanced Encryption Standard)

[prema 18, 19, 20]

AES algoritam je algoritam za zaštitu digitalnih podataka, a razvijen je na temelju poznatog Rijndael algoritma. Osnovna mu je zadaća, kao i IDEA algoritmu, da naslijedi DES, čije karakteristike danas više ne zadovoljavaju vrlo visoke kriterije koji se nameću na kriptografske sustave.

Algoritam su 1998. godine razvila dvojica belgijskih kriptografa Vincent Rijmen i Joan Daemen pa se često naziva i Rijndael, no to nije u potpunosti točno. Algoritam u originalu pruža dodatnu fleksibilnost jer omogućuje odabir veličine ključa i bloka od 128, 192 ili 256 bitova, no AES algoritam po standardu omogućuje kriptiranje 128-bitnih blokova s ključevima duljine 128, 192 ili 256 bitova pa se s obzirom na duljinu ključa razlikuje AES-128, AES-192 i AES-256. Slično kao i DES, AES je razvijen u privatnom sektoru, no u suradnji s američkom vladom. AES je definiran i prihvaćen od strane NIST-a 2001. godine te se kao takav može koristiti u američkim državnim i drugim institucijama, a 2002. je uvršten u ISO/IEC 18003-3 standard.

Ovo je relativno jednostavan algoritam koji ima više krugova izvođenja, ovisno o veličini ključa:

• 10 krugova izvođenja ako je ključ veličine 128 bitova,
• 12 krugova izvođenja ako je ključ veličine 192 bita,
• 14 krugova izvođenja ako je ključ veličine 256 bitova.

Svaki krug izvođenja obuhvaća četiri koraka:

1. Zamjena okteta na temelju supstitucijske tablice (S-blok).
2. Posmak redaka u matrici stanja.
3. Miješanje podataka unutar svakog stupca matrice stanja.
4. Dodavanje podključa u matricu stanja.

Šifriranje se provodi tako da se ulazni blok kopira u matricu stanja veličine 4×4 te se zatim provodi inicijalno dodavanje podključa u matricu. Nakon toga, matrica stanja se transformira, opet ovisno o duljini ključa:

• za 128-bitni ključ, matrica stanja se transformira 10 puta,
• za 192-bitni ključ je potrebno 12 transformacija matrice stanja,
• za 256-bitni ključ radi se 14 transformacija matrice stanja.

Naglasak jest na tome da se posljednji korak donekle razlikuje od prethodnih. Ključ se prikazuje kao određeni broj 32-bitnih riječi koji, ovisno o duljini, varira pa može biti predstavljen s 4, 6 ili 8 riječi. Konačno, matrica stanja se kopira u izlazni blok. Četiri okteta u svakom stupcu matrice stanja formiraju 32-bitnu riječ. Dešifriranje se izvodi na sličan način, ali uz upotrebu inverznih funkcija.

U najnovije vrijeme pronađene su kriptografske metode koje teoretski omogućavaju i razbijanje AES algoritma u vremenu bržem od napada primjenom sile (eng. brute force). Naime, iako AES nije osjetljiv na napade korištenjem linearne i diferencijalne kriptoanalize, postoje naznake da je osjetljiv na algebarske napade, a posebno na novu XSL (engl. eXtended Sparse Linearization) metodu napada. Usprkos tome, svakako je potrebno naglasiti i prednost što u algoritmu do sad nisu pronađeni nesigurni ili potencijalno nesigurni ključevi (kao npr. kod DES-a i IDEA algoritma).

Kriptoanaliza

Kao što možemo vidjeti kroz povijest, kriptografija se razvijala i smišljali su se što bolji načini kako bi se osigurala tajnost podataka. Iz početka su to bili jednostavni algoritmi koji su se lako razbijali, ali kako je vrijeme odmicalo, napretkom matematičkih znanosti, kriptiranje je postalo sve složenije. Sa sve složenijim kriptiranjem i algoritmi za dekriptiranje, a samim time i probijanje šifre bez šifrata, zahtijevalo je puno više vremena, ali i znanja te memorijskog prostora kako bi se došlo do izvornog teksta.

Bez obzira na tu činjenicu, skoro pa paralelno s pojavom složenih kriptografskih algoritama, pojavile su se i metode koje dovode do dekriptiranja kriptiranog teksta. Takve metode spadaju u znanstvenu disciplinu koju zovemo kriptoanaliza. Naziv potječe od dvije grčke riječi: kryptós – skriven i analýein – odriješiti.

Ponekad se naziv kriptoanaliza koristi za pokušaj zaobilaženja sigurnosti kriptografskih algoritama ili protokola, a ne samo za kriptografsku zaštitu što bi joj trebao biti glavni cilj, pa tako kriptoanaliza obično uključuje metode napada koje ne ciljaju na ranjivost poput socijalnog inženjeringa ili krađe.

Metode i tehnike kriptoanalize drastično su se promijenile tijekom povijesti, a razlog je vrlo jednostavan - napredak same kriptografije. Također, može se reći da se promijenio i rezultat kriptoanalize, u smislu da više nije moguće imati gotovo neograničen uspjeh u probijanju kodova. Probijanje kriptografskog algoritma daje nam tajne informacije odnosno ključeve koji se koriste za dešifriranje kriptiranog teksta. Za pronalaženje asimetričnih ključeva najčešće se koristi fakorizacija cjelobrojnih brojeva.

Povijest kriptoanalize

Kako je već napomenuto, kriptoanaliza se razvijala zajedno s kriptografijom kako bi pokušala spriječiti stare načine probijanja šifri, odnosno kako bi se u poboljšanoj verziji smanjila vjerojatnost toga da tajni podaci budu pročitani od neželjene osobe. „U praksi, kriptografija i kriptoanaliza odnose se kao dvije strane istog novčića: kako bi se kreirala sigurna kriptografija, potrebno je dizajn prilagoditi mogućim kriptoanalizama.“ [2] Postoje četiri opća tipa kriptoanalitičkog napada. Naravno, za sva četiri tipa pretpostavlja se da kriptoanalitičar ima sve potrebno znanje o kriptiranju koje koristi algoritam:

1. Napad “samo šifrat” (eng. 'ciphertext-only attack') - Kriptoanalitičar ima kriptirano nekoliko poruka koje su kriptirane istim algoritmom za kriptiranje. Zadatak kriptoanalitičara je da rekonstruira otvoreni tekst što većeg broja poruka ili, još bolje, da otkrije ključ koji se koristi za kriptiranje poruka kako bi dekriptirao druge poruke kriptirane istim ključem.

2. Napad “poznat otvoreni tekst” (eng. 'known-plaintext attack') - Kriptoanalitičar ima pristup šifratima za nekoliko poruka, kao i otvorenim tekstovima tih poruka. Njegov je posao da izračuna ključ korišten za kriptiranje poruka ili algoritam, kako bi dešifrirao svaku novu poruku kriptiranu istim ključem.

3. Napad “odabran otvoreni tekst” (eng. 'chosen-plaintext attack') - Kriptoanalitičar ne samo da ima pristup šifratu i pripadajućem otvorenom tekstu nekoliko poruka, već i bira otvoreni tekst koji će biti kriptiran. Ovo je moćnije od napada “poznat otvoreni tekst” jer kriptoanalitičar može odabrati specifične blokove otvorenog teksta za kriptiranje i tako doći do više informacija o ključu. Njegov je posao da izračuna ključ koji se koristi za kriptiranje poruka ili da odredi algoritam pomoću koga bi dešifrirao svaku novu poruku kriptiranu istim ključem.

4. Napad “prilagodljiv odabrani otvoreni tekst” (eng. 'adaptive-chosen-plaintext attack')- Ovo je poseban slučaj napada “odabran otvoreni tekst”. Ne samo da kriptoanalitičar može odabrati kriptiran otvoreni tekst, već može i modificirati ono što je odabrao na osnovu rezultata prethodnih kriptiranja. Prilikom napada “odabran otvoreni tekst” kriptoanalitičar može odabrati da kriptira jedan veliki blok otvorenog teksta, dok u napadu “prilagodljiv odabrani otvoreni tekst” može odabrati manji blok otvorenog teksta, a zatim još jedan na osnovu rezultata prvog i tako dalje. Važno je napomenuti da se snaga sigurnosti kriptosustave ne povećava činjenicom da napadač ne zna koji se sustav za kriptiranje koristi. Baš naprotiv, poznati algoritmi se svakim danom sve više i više štite te kriptografi i kriptoanalitičari surađuju kako bi se poruke što bolje zaštitile. [Prema 10]

Kako bi se postigla sigurnost kriptografskog algoritma:

• cijena “razbijanja” algoritma mora biti veća od cijene šifriranih podataka,
• vrijeme potrebno za “razbijanje” algoritma mora biti duže od vremena u kojem podaci moraju ostati tajni,
• broj podataka šifriranih jednim ključem mora biti manji od broja potrebnih podataka kako bi se dani algoritam “razbio”.

Klasična kriptoanaliza

Sam izraz kriptoanaliza je relativno nov, a uveo ga je William Friedman 1920. godine. Međutim, probijanje šifri i metode probijanja šifri puno su starije. Prvo poznato zapisano objašnjenje kriptoanalize dao je u 9. stoljeću arapski matematičar Al-Kindi, poznat po nazivu Alkindus u djelu „A Manuscript on Deciphering Cryptographic Messages“ („Rukopis o dešifriranju kriptografskih poruka“). [Prema 2]

Za probijanje najvećeg dijela klasičnih šifri upotrebljava se analiza učestalosti. Princip analize učestalosti je zapravo vrlo jednostavan: promatra se učestalost pojavljivanja određenih slova nekog jezika. U engleskom jeziku najčešće se pojavljuje slovo „E“. Analiza učestalosti oslanja se na činjenicu da šifre obično ne skrivaju takvu statistiku. Na primjer, u običnom kriptiranom tekstu, slovu koje se najčešće pojavljuje pridjeljuje se vrijednost slova „E“. Ovo je poprilično jednostavna analiza ako je kriptirani tekst dovoljno dugačak za provođenje analize.

Uvidjevši problem, tijekom 15. i 16. stoljeća, razvijena je ideja o abecednoj zamjeni znakova (eng. polyalphabetic substitution cipher), a jedan od pokretača bio je Blaise de Vigenère. Naredna tri stoljeća Vigenèreova šifra se koristila kao ključ koji se sastojao od proizvoljne riječi za odabir različitih kriptirajućih abeceda. Funkcioniralo je tako da se svako slovo nekriptiranog teksta zamijeni nekim drugim. Takve šifre smatrale su se u potpunosti sigurnim. Međutim, Charles Babbage i, kasnije, Friedrich Kasiski uspjeli su probiti spomenutu šifru. [Prema 2] Tijekom Prvog svjetskog rata izumitelji su u nekoliko država razvili kružne mehanizme šifriranja (eng. rotor cipher machines) u nastojanju da minimiziraju ponavljanje koje je dovelo do proboja Vigenèreova sustava.

Prikupljanje informacija o porukama ponekad može biti tehnika kriptoanalize sama po sebi. Naime, dobivanjem podataka o porukama koje se šalju te ključevima, može se dešifrirati poruka pa napadač može jedno vrijeme raditi u pozadini, odnosno skrivati se pa osobe koje sudjeluju u komunikaciji, tj. razmjeni poruka, nisu ni svjesne da netko vanjski čita te iste poruke ili da ih ima mogućnost mijenjati. Problem se javio pojavom sve složenijih algoritama za kriptiranje čime je matematika postala sve važnija u kriptoanalizi. To se najbolje moglo vidjeti neposredno prije i za vrijeme Drugog svjetskog rata, zbog napora da se probijaju šifriranja Sila Osovine, odnosno agresora. Kasnije se pokazalo da je kriptoanaliza pridonijela bržem završetku rata. Naime, Njemačka je bila sigurna da se šalju poruke koje su sigurne, međutim njihove poruke su bile presretane i pročitane tako da neki stručnjaci smatraju da je rat završio i dvije godine ranije zbog toga. Najpoznatiji stroj za kriptiranje i dekriptiranje teksta tog vremena bio je Enigma.

Strojevi za dekriptiranje šifri poput Lorenzove šifre i stroja Enigma koji se koristio od strane nacističke Njemačke tijekom Drugog svjetskog rata, imali su poruke kod koje je svaka poruka imala svoj ključ. Kako se taj ključ mijenjao trebalo je svaki put podesiti stroj da bi se mogla pročitati poruka. Obično je pošiljatelj informirao primatelja o ključu poruke tako što je napisao neki obični tekst prije kriptirane poruke. Taj termin se zove indikator koji je indicirao odnosno pokazivao primatelju kako da postavi stroj da dekriptira poruku.

Bio je to dosta loše dizajniran i implementiran indikator jer su brzo Poljaci, a kasnije i Britanci, slomili sustav Enigma šifri. Slični slabi sustav indikacija dopustio je Britancima da identificiraju dubinu koja je vodila do dijagnoze Lorenz SZ40/42 sustava i sveukupno provaljivanje njegovih poruka bez da su kriptoanalitičari vidjeli stroj.

Moderna kriptoanaliza

Moderna kriptografija postala je neprobojna za poznate metode kriptoanalize, odnosno više se nije moglo probijati šifru bez uporabe računala. David Kahn je u svom djelu o kriptoanalizi naveo mnoge mogućnosti zamjene tradicionalne kriptoanalize poput presretanja poruka. Navodi kako mnogi proizvođači nude kriptografske sustave koje nije moguće probiti poznatim metodama kriptoanalize. U takvim sustavima, ključ nije moguće otkriti usporedbom nekriptiranog teksta s kriptiranim. [Prema 2]

Kod simetričnog ili konvencionalnih kriptosustava, ključ za dekriptiranje može se izračunati poznavajući ključ za kriptiranje i obrnuto, obično su ova dva ključa identična. Postoje dvije vrste napada na simetrično kriptirane poruke. To su diferencijalna kriptanaliza i linearna kriptoanaliza na koju ćemo se posebno osvrnuti u ovom radu.

Diferencijalnu kriptanalizu prvi su javno predstavili i objavili Eli Biham i Adi Shamir. Neposredno nakon objave ovog rada autori koriste opisani napad kako bi razbili cijeli niz do tada sigurnih kriptoalgoritama: već iste godine razbijaju Snefru, Khafre, REDOC-II, LOKI i Lucifer. Diferencijalna kriptoanaliza potiče pravu eksploziju kriptoanalitičkih metoda u devedesetim godinama - pojavljuje se velik broj proširenja ili modifikacije diferencijalne kriptoanalize (primjerice bumerang i inside-out napadi, slide napad, diferencijalni napad povezanim ključem, itd.). Međutim ova metoda bila je i prije poznata. IBM i NSA su znali za ovaj napad već 1974. godine, međutim nisu ga objavljivali te je time SAD bio u velikoj prednosti naspram drugih. Metoda spada u napade „odabrani otvoreni tekst“. [Prema 2]

O linearnoj kriptoanalizi bit će više riječi u nastavku pa se ovdje ne će posebno spominjati.

Asimetrična kriptografija oslanja se na uporabu dva ključa, jednog privatnog i drugog javnog. Probijanje takvih šifri zasniva se na rješavanju kompleksnih matematičkih problema. Na primjer, sigurnost sheme za razmjenu ključeva Diffe-Hellman ovisi o složenosti računanja diskretnih logaritama. 1983. godine Don Coppersmith pronašao je brži način određivanja diskretnih algoritama u pojedinoj grupi što je dovelo do potrebe za uporabom većih grupa u kriptografiji. [Prema 2]

Jedan od očitih napada RSA je faktorizacija pa sigurnost algoritma RSA ovisi o složenosti faktorizacije cjelobrojnih brojeva. 1980. godine bilo je moguće faktorizirati broj od 50 digitalnih znamenki na računalu sa 1012 osnovnih računalnih operacija. Do 1984. godine, s istim utroškom računalnih resursa, bilo je moguće faktorizirati broj sa 75 digitalnih znamenki. Napredak u računarskoj tehnologiji također je značio brže obavljanje operacija na računalima. Na brzim, modernim računalima stručnjaci su uspjeli faktorizirati brojeve sa 150 digitalnih znamenki pa se takva duljina ključa, od početka 21. stoljeća, ne smatra dovoljnom za sigurnost algoritma RSA. Međutim brojevi od preko 250 znamenaka zasad su sigurni od ovog napada. [Prema 2]

Da bi zaštitili svoje poruke koje putuju nesigurnim kanalom koristimo kriptiranje. Također može se pretpostaviti, pošto je kanal nesiguran, da prisluškivači kanala imaju kompletan pristup komunikacionim kanalima između pošiljatelja i primatelja. Da bi našu poruku pročitao netko s treće strane, mora imati ključ ili određeno znanje na koji način će doći do izvornog teksta. Kriptoanaliza je nauka koja bez ključa određuje otvoreni tekst na osnovu šifrata, tako da ukoliko treća strana zna uspješno primjenjivati kriptanalizu može rekonstruirati otvoreni tekst ili ključ. Kriptoanaliza nam također služi za otkrivanje nedostataka i slabosti u kriptosustavu. Osnovna pretpostavka kriptoanalize, koju je prvi objavio A. Kerkhof, jest da tajnost mora biti potpuno zasnovana na ključu. Kerkhof je pretpostavio da kriptoanalitičar zna sve pojedinosti kriptografskog algoritma i njegove primjene.

Linearna kriptoanaliza

Povijest linearne kriptoanalize

Linearna kriptoanaliza je napad predstavljen od strane Mitsuru Matsuija 1993. godine na Eurocryptu, kao teorijski napad za razbijanje DES algoritma, iskorištavanjem specijalne povezanosti između ulaznih i izlaznih blok šifri. Napad prati statističke korelacije između informacija o otvorenom tekstu i šifriranom tekstu pomoću vjerojatnosnih linearnih izraza, odnosno koncepta koji su ranije predstavili Corfdir i Gilbert. Ubrzo nakon toga dogodilo se nekoliko pokušaja generaliziranja linearne kriptoanalize, a jedan takav objavljen je od strane Kalinskog i Robshawa koji su pokazali kako je moguće kombinirati nekoliko nezavisnih linearnih korelacija, ovisno o istim bitovima ključa. Vaudenay pak s druge strane, predstavlja drugi oblik napada na DES, nazvan dvostruki napad. Njime pokazuje da napad može biti nešto manje snažan nego linearna kriptoanaliza, bez da se zna što se točno događa u blok šifri. Praktični primjeri napada su Knudsenov i Robshawov napad na LOKI91 i Shimoyamin i Kanekov napad na DES. U oba napada se koriste nelinearne aproksimacije. Harpes i Massey generalizirali su rezultat s obzirom na particije parova ulaznih i izlaznih prostora. Neka su X={x1,x2,…,xn} i Y={y1,y2,…yn} particije ulaznih i izlaznih skupova gdje se xi i yi nazivaju blokovi. Par (X,Y) zove se par particije, ako svi blokovi od X odnosno Y sadrže isti broj otvorenog teksta odnosno šifriranog teksta. Analiziranje particija iskorištava činjenicu da se vjerojatnosti oblika Pr [(X,fk(X) element (X,Y))] ne mogu ravnomjerno rasporediti za svaki blok šifre fk kad je otvoreni tekst X ravnomjerno raspoređen. Kako bi opisali tu nejednakost u raspoređivanju, Harpes i Massey razmotrili su dvije mjere nazvane vršna ravnoteža i Euklidova kvadratna neravnoteža. Harpes i Jakobsen razvili su korisne stvari za procjenu otpornosti blok šifri pri analizi particija kriptosustava. Prvi najbolji praktični primjer particioniranja kriptosustava radi probijanja blokova šifri jest napad na Crypton poznat kao „stohastička kriptoanaliza“, a predstavili su ga Miner i Gilbert. U nekoliko radova prikazana je snaga linearnih i nelinearnih aproksimacija baziranih na različitim algebarskim strukturama. Standaert je iskoristio linearne aproksimacije prostora Z4 rekombiniranjem vrijednosti kako bi se problem sveo na poznati binarni slučaj. [Prema 1]

Općenito o linearnoj kriptoanalizi

Kako postoje simetrični algoritmi za enkripciju, tako se neki koriste za napad na blokovske kriptografske sustave koji nekriptirani tekst dijele u blokove i zatim koriste posebne funkcije za miješanje bloka teksta s ključem čime se dobije šifrirani tekst. Linearna i diferencijalna kriptoanaliza su dva najznačajnija napada za probijanje simetričnog ključa. Napadima na kriptosustave cilj je saznati tajni ključ K. Linearna i diferencijalna kriptoanaliza ne napadaju kriptosustav izravno, već umjesto toga, analiziraju slabosti dizajniranih blokova šifri. Ove tehnike općenito ne daju kao rezultat praktični napad. Danas su te tehnike postale osnovni analitički alati koji se primjenjuju kod analiziranja svih blokova šifri. Oba algoritma su prvotno razvijeni za napad na DES stoga nije precijenjen njegov utjecaj na modernu kriptografiju.

DES je donedavno bio standardni algoritam za enkripciju i bio je najčešće korišten simetrični algoritam. Razvijen je u IBM-u 1977. godine. Može se upotrijebiti kao block chiper (za blok šifriranje), a koristi duljinu blokova od 64 bita za šifriranje i ključ veličine 56 bita (64 bitni prikaz ključa, ali se svaki osmi bit zanemaruje ili služi za provjeru pariteta). Do kraja devedesetih bio je enkripcijski standard i zadovoljavao je ciljeve sigurnosti. Ipak pokazalo se, i potvrđeno je, razbijanje tog algoritma (npr. brute force napad), stoga se danas koristi u obliku TripleDES (3DES) koji se smatra vrlo pouzdanim i unaprjeđuje sigurnost. U biti, taj je algoritam modifikacija u kojoj se isti blok tri puta kriptira koristeći orginalan DES algoritam. TripleDES koristi 2 ili 3 različita ključa čime se povećava broj kombinacija za pronalaženje ključa. Blok podataka izvorne poruke kriptira se prvim ključem zatim se ta kriptirana poruka dekriptira drugim ključem čime se dobije nova kriptirana poruka te se nakraju rezultat dekripcije opet enkriptira trećim ili prvim ključem.

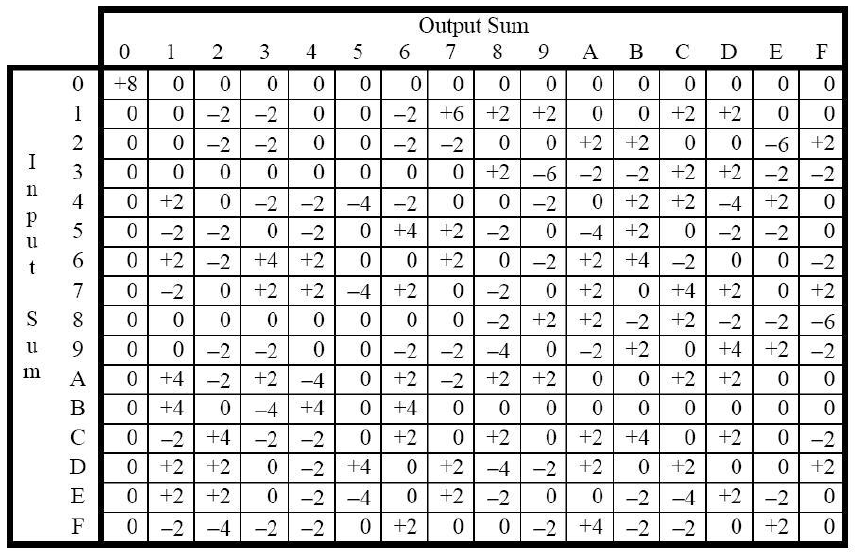
Za kratki pregled linearne kriptoanalize neće nam trebati svi detalji DES-a, stoga je prikazan pojednostavljeni pogled koji uključuje neophodne činjenice. Kod DES algoritama pojavljuje se osam S-blokova od kojih svaki mapira šest ulaznih bitova koji imaju oznake x0x1x2x3x4x5 u 4 izlazna bita označenih sa y0y1y2y3. Npr. prvi DES S-blok u heksadecimalnom zapisu je:

Primjer prvog S-bloka DES-a Izvor: Stamp M. (2006). Information Security principles and practice. John Wiley & Sons, str. 111

Primjer iznad prikazuje pojednostavljeni pogled na DES što će biti dovoljno za daljnje objašnjenje. Kako je linearna kriptoanaliza fokusirana na analizu nelinearnih dijelova DES-a, slika iznad samo naglašava da su S-blokovi jedini nelinearni dio u DES-u. Tablica također prikazuje način na koji podključ Ki ulazi u DES ciklus (eng. round). U nastavku će biti prikazan opći pregled linearne kriptoanalize.

Linearna kriptoanaliza je malo realniji napad nego diferencijalna kriptoanaliza jer je prvenstveno poznata kao napad poznatim otvorenim tekstom umjesto napad odabranim otvorenim tekstom te je također konceptualno jednostavnija. Ironično nazivu linearna, usmjerena je na analiziranje nelinearnih blok šifri odnosno pronalaženje srodnih približnih vrijednosti šifri uz pomoć linearnih jednadžbi (aproksimacija). Pošto su matematičari dobri u rješavanju linearnih jednadžbi i ukoliko se mogu pronaći takve aproksimacije, logično je da se može koristiti iza napad na kriptosustav odnosno probijanje ključeva. Kako su jedini nelinearni dio DES-a njegovi S-blokovi, linearna kriptoanaliza je fokusirana na njih. Vratimo se ponovno na prethodnu sliku. Označena su tri ulazna bita sa x0x1x2 i dva izlazna bita sa y0y1. Nadalje x0 određuje red, a x1x2 stupac. Na slici ispod vidi se broj vrijednosti koji svaka linearna aproksimacija posjeduje.

Linearna analiza S-bloka Izvor: Stamp M. (2006). Information Security principles and practice. John Wiley & Sons, str. 114

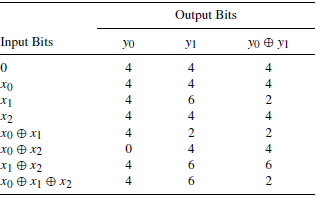
Budući da postoji 8 izlaznih vrijednosti u svakom slučaju, bilo koji broj osim četiri, označava neslučajan izlaz. Rezultati u tablici iznad pokazuju da je primjerice y0 = x0 xor x2 xor 1 ima vjerojatnost 1 i y0 xor y1 = x1x2 vjerojatnost 3/4. Koristeći takve podatke, S-blokovi se mogu zamijeniti linearnim funkcijama. Rezultat je ustvari „pretvaranje“ nelinearnih S-blokova u linearne jednadžbe gdje linearne jednadžbe zadržavaju neke vjerojatnosti. Takve linearne aproksimacije mogu biti korisne u napadu na blok šifre poput DES. Kako se mogu što bolje aproksimirati S-blokovi sa linearnim funkcijama? Svaki S-blok je dizajniran tako da je nelinearna kombinacija ulaza, dobra aproksimacija za jedan izlazni bit. Međutim, postoje i linearne kombinacije izlaznih bitova koji se mogu aproksimirati linearnim kombinacijama ulaznih bitova. Kao rezultat toga postoji potencijal za uspjeh napada linearne kriptoanalize na DES. [Prema 1]

Matematička pozadina linearne kriptoanalize

Sada ćemo pokazati i pokušati što detaljnije objasniti matematičku pozadinu same linearne kriptoanalize. Što u biti linearna kriptoanaliza pokušava napraviti? Ona nastoji iskoristiti prednost velikog broja ponavljanja linearnih izraza koji uključuju bitove ne kriptiranog teksta, bitove kriptiranog teksta i bitove pod ključeva.

Prvo ćemo pojasniti supstitucijsko-permutacijsku mrežu. Ukoliko se sjećate, kod supstitucije dolazi do zamjene ulaznih bitova, dok kod permutacije dolazi do razmještanja ulaznih bitova. U svrhu što jasnijeg pojašnjenja matematičke strane, reducirat ćemo duljinu koda sa 64 bita na 16 bita, zatim ćemo maknuti funkciju proširenja. Ona je bila objašnjena u opisu funkcioniranja DES algoritma i radili smo je prema E-bit selection table. Također ćemo koristiti identične S kutije veličine 4 bita i ponavljat ćemo s manjim brojem rundi.[Prema 23]

Jednostavna supstitucijsko-permutacijska mreža

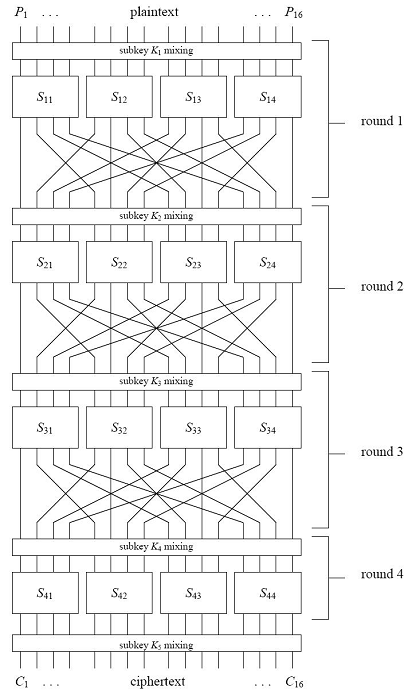
Konstruirat ćemo jednostavnu mrežu koja je strukturalno slična DES algoritmu. Mreža koristi 16 bitni ne kriptirani tekst te 16 bitni kružni ključ, kako bi ga pretvorila u 16 bitni kriptirani tekst. Svaka runda (ponavljanje) se sastoji od supstitucije i permutacije, isto kao i u DES-u. Supstitucija će biti rezultat djeljenja 16 bitnog bloka na 4 jednaka dijela od po 4 bita. Ta 4 bita ćemo dalje usmjeriti na jednake S kutije. Miješanje ključa je postignuto operacijom XOR kružnog ključa. Mreža koju ćemo promatrati sastojat će se od 4 runde.

S kutija koju ćemo koristiti:

Tablica za permutacije koju ćemo koristiti:

Korištenjem ovih tablica za supstitucije i permutacije ova mreža je sa kriptografske strane slična DES algoritmu.

Kako bi mogli što lakše razumjeti matematičku pozadinu definirat ćemo varijable koje ćemo koristiti u objašnjenju.

Pi - i ide od 1do 16, koristit ćemo ga kao i-ti bit ne kriptiranog teksta

Ci - i ide od 1do 16, koristit ćemo ga kao i-ti bit kriptiranog teksta

Uj,i - j ide od 1 do 4, i ide od 1 do 16, i-ti ulazni bit u j-tu rundu mreže

Vj,i - j ide od 1 do 4, i ide od 1 do 16, i-ti izlazni bit u j-toj rundi mreže

Kj,i - j ide od 1 do 4, i ide od 1 do 16, i-ti kružni ključ za j-tu rundu(ponavljanje) mreže

Prvo moramo pogledati jedine ne linearne elemente mreže. To su S kutije, konkretno u našem slučaju promatramo samo jednu. Kako bi pronašli linearno povezanu aproksimaciju S kutije, jednostavno uzmemo u obzir svaki mogući izraz ulaznih bitova Xi i izlaznih bitova Yi.

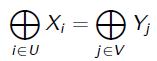
U i V nam predstavljaju raspon od svih mogućih elemenata podskupa 1,2,3,4. Nakon toga usporedimo koliko često se izraz podudara sa S kutijom. Možemo primijetiti kako imamo 16 mogućnosti za U i V, dakle ukupno 256 mogućih izraza za 4 bitnu S kutiju. Za primjer ćemo uzeti sljedeći izraz.

Primjenjujući sve moguće vrijednosti za ulaznih X bitova ispada da izraz sadržava 12 od mogućih 16 slučajeva. Ovaj izraz ima odstupanje od 12/16 - 1/2 = 1/4.

Prethodni izraz ima odstupanje od -3/8, što je više nego prethodni. Ovdje je veličina odstupanja ta koja je važna. Sada slijedi prikaz tablice odstupanja.

Kako bi dobili odstupanje, vrijednost trebamo podijeliti sa 16, iz razloga što imamo 16 mogućnosti. Sada ćemo to malo prikazati na prvoj rundi (ponavljanju). Idemo to prikazati na prvoj rundi.

Iz slike možemo vidjeti sljedeće:

Ukoliko to izračunamo prema tablici odstupanja, vidimo da izraz ima odstupanje od 3/4. Moramo paziti da je X1 u biti sljedeći izraz.

Možemo napisati sljedeću linearnu aproksimaciju kroz prvu rundu mreže.

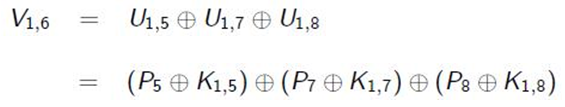
Možemo dobiti izraze koji sadržavaju 1/4 šanse pojavljivanja, što je suprotno šansi od 3/4. No u biti mi njih moramo nekako iskombinirati kako bi na kraju dobili izraz koji dovodi u vezu kriptirane bitove teksta i ne kriptirane bitove teksta. Za to se koristi Pilling Up princip kojega ovdje nećemo objašnjavati.

Slika je prikazana kako bi se vidjelo gdje se nalazi koja S kutija. Možemo zapisati 4 aproksimacije, odnosno 4 izraza.

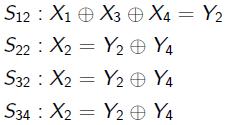
Svaki od tih izraza ima veličinu odstupanja 1/4. Pomoću Pilling up principa možemo ih iskombinirati u jedan izraz koji dovodi u vezu kriptirane bitove teksta i ne kriptirane bitove teksta. U obzir ćemo uzeti prva dva izraza.

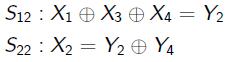
Kada ta dva izraza spojimo dobijemo sljedeći.

Prema Pilling up principu i budući da smo iskombinirali dva izraza od kojih svaki ima odstupanje od 1/4, sada oni zajedno imaju odstupanje od 1/8. Dalje koristeći princip možemo napisati sljedeću jednadžbu preko 3 runde mreže.

Suma K je suma nekih bitova ključa. Kako znamo da je ključ fiksan, suma može biti ili 0 ili 1 i kao takvu ju možemo ignorirati iz razloga jer nas zanima samo odstupanje. Veličina odstupanja prethodnog izraza prema Pilling up principu je 1/32. To ćemo sada iskoristiti, iz razloga jer je odstupanje jako daleko od 1/2, te ćemo prikazati kako izvući informacije o ključu. Iz prethodnog izraza možemo parcijalno vratiti zadnju rundu tako što ćemo pogoditi zadnji ključ. Ukoliko pogodimo, jednadžba će zadržati veliko odstupanje, a ukoliko pogriješimo jednadžbi će se odstupanje promijeniti blizu 1/2, odnosno na nulto odstupanje. Ne moramo pogađati cijeli ključ za zadnju rundu. Vidimo da izraz uključuje 4 ulazna bita u četvrtoj rundi i izlaz iz dvije S kutije u trećoj rundi. Moramo pogađati samo 256 vrijednosti. Za svaku pogođenu parcijalnu vrijednost pod ključa, možemo vratiti zadnju rundu i odrediti odstupanje jednadžbe. Što veće odstupanje, veća je šansa da smo pogodili.

Za aproksimaciju koju smo mi ovdje imali, odnosno za odstupanje od 1/32 bi nam trebalo 1000 parova kriptiranog - ne kriptiranog teksta, kako bi izveli napad sa skoro 100% šanse za uspjeh.[Prema 23]

Pregled osnovnog napada linearne kriptoanalize

Linearna kriptoanaliza pokušava iskoristiti visoku vjerojatnost pojave linearnih izraza koji uključuju bitove otvorenog teksta, bitove šifriranog teksta i bitove podključa. To je poznato kao napad otvorenim poznatim tekstom, a zapravo znači da napadač ima informacije o skupu otvorenog teksta i odgovarajućih šifriranih tekstova. Međutim, nema načina na koji bi napadač otkrio koji su otvoreni tekstovi s odgovarajućim šifriranim tekstovima dostupni. Uobičajena je pretpostavka da napadač ima znanje o slučajnim skupovima otvorenog teksta i odgovarajućeg šifriranog teksta. Linearna kriptoanaliza provodi se u dva koraka:

1. korak - pronalaženje linearne aproksimacije šifre
   1.1. Pronaći linearne izraze koji su dobra aproksimacija nelinearnim dijelovima šifre (S-blokovi). 
   1.2. Proširiti linearnu aproksimaciju na cikličku funkciju (eng. round function) čime se dobiva linearni izraz za svaku aproksimaciju.
   1.3. Konstruirati linearnu aproksimaciju kriptosustava sastavljanjem linearnih jednadžbi za cikličku funkciju (eng. round function). 
        Vjerojatnost ove aproksimacije kriptosustava može se izračunati iz vjerojatnosti aproksimacija dobivenih u svakom ciklusu.
   1.4. Izračunati broj poznatih otvorenih tekstova potrebnih za dobivanje izraza linearne aproksimacije.

2. korak - primjena algoritma poznatim otvorenim tekstom.

Znači, osnovna ideja jest da se aproksimira (približi) dio kriptiranog teksta s linearnim izrazom gdje se linearnost odnosi na modulo 2 bitovne operacije (ekskluzivno ili, XOR). Takav izraz je oblika:

</center></center>

Gdje xi predstavlja i-ti bit ulaza X=[x1,x2,…], a yi predstavlja j-ti bit izlaza Y =[y1,y2]. Ta jednadžba predstavlja ekskluzivno ili „sumu“ u bitova unosa i v bitova izlaza. Koncept je određivanje izraza gornjeg oblika koji imaju veću ili manju vjerojatnost pojave. Kažemo da kriptosustav ima slabi generator slučajnih brojeva, ako šifra teži tome da gornja jednadžba (*) vrijedi sa velikom vjerojatnošću ili da ne vrijedi sa velikom vjerojatnošću. Ako bi slučajnim odabirom uzeli vrijednosti za u+v bitove i uvrstili ih u gornju jednadžbu, vjerojatnost da će izraz vrijediti bila bi točno ½. Što je vjerojatnost da će izraz vrijediti dalja od ½ , to je primjenjivost kriptoanalize bolja. [Prema 6]

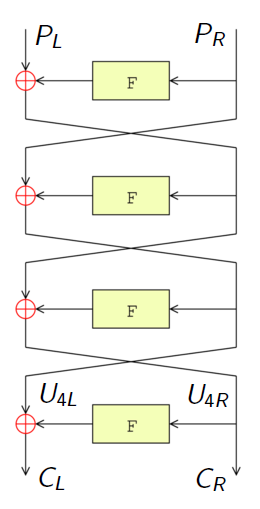
Linearna kriptoanaliza kriptosustava kriptiranog jednostavnom zamjenom (eng. toy cipher)

Ovo je zabavan vodič Jona Kinga koji za sebe kaže da je naučio jezik matematike i kriptografije te je ideju tehnike pokušao objasniti na pristupačan i razumljiv način. Pretpostavljeno je osnovno poznavanje tipičnih simbola i značenja nekih pojmova. Prvo će biti objašnjeno, zašto bi se napad trebao izvršiti na slijedeći način. Na slici ispod nalazi se kriptosustav kriptiran jednostavnom zamjenom (eng. toy cipher) koji će nakraju biti razbijen.

Kriptosustav kriptiran jednostavnom zamjenom Izvor

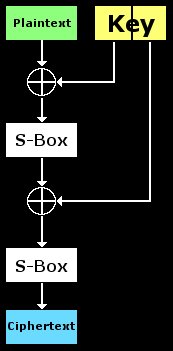
Kao što se vidi sa slike, sastoji se od dva ciklusa (eng. round). U svakom ciklusu, na ulazu se vrši operacija xor otvorenog teksta sa dijelom ključa nakon čega prolazi kroz S-blok (eng. S-box). Na umu treba imati da se barata sa 16 parova poznatog otvorenog i njemu pripadajućeg šifriranog teksta. Svi ovi parovi šifrirani su istim ključem. Također poznato nam je kako funkcioniraju S-blokovi (eng. S-box) i da je u njima jedino nepoznat - ključ. Koristit će se i neke statističke informacije o S-blokovima i neka testiranja enkripcije za obnovu ključa sa mnogo manje uloženog truda nego npr. kod brute force napada koji provjerava sve postojeće ključeve.

Zamislite da je jedino lijeva polovica ključa korištena i da postoji samo jedan ciklus kod ovog kriptosustava. On se trivijalno može „razbiti“ na slijedeći način – vraćanjem šifriranog teksta unatrag kroz S-blokove a zatim ga xor operacijom vratiti u otvoreni. Taj postupak rezultira otkrivanjem ključa poznavanjem samo jednog para bez napora. Ako se tehnika ponovi u dva ciklusa, događa se slijedeće. Prvo je šifrirani tekst prošao unatrag kroz drugi S-blok, zatim je prije ulaza u drugi ciklus na njemu izvršena xor operacija. Napomena je da se ne zna što je zapravo ulaz u drugi ciklus. U cilju dobivanja informacije, potrebno je znati što je izlaz iz prvog ciklusa, a time i lijevu polovicu ključa. Pretpostavka je da se lijeva polovica ključa može opraviti (eng. key recover), a zatim će se prijeći na desnu polovicu. Sada se uzima poznati otvoreni tekst i na njemu se vrši xor operacija sa pretpostavljenom lijevom polovicom ključa. Nadalje prolazi kroz prvu S-tablicu i sada imamo pretpostavljen izlaz iz prvog ciklusa. Ali, taj izlaz se nema s čim usporediti. Također se ne zna da li je taj izlaz točan i na taj način se ne može dalje upotrijebiti. Ako pokušate izvršiti oporavak ključa (eng. key recover) bez testiranja svakog pojedinog ključa koristeći različite jednostavne tehnike, vidjet će se zašto ne funkcioniraju. To je jedini način da se uvidi da je potrebno drugačije rješenje. Ukoliko bi se bavili sa gornjim kriptosustavom, vidjeli bi smisao da se šifra kreirana kroz dva ciklusa puno teže probija nego ona iz jednog.

Detalji kriptosustava kriptiranog jednostavnom zamjenom

S-blok kriptosustava Izvor

Iznad su definirani neki parametri koje kriptosustav koristi, a kasnije će biti upotrijebljeni. Ovi parametri kriptosustava mogu se podići na višu razinu koja se može koristiti u praksi. Veličina bloka je 4 bita, a veličina ključa 8 bita što daje 2*4 podključeva. To znači da se svaki 4-bitni blok miješa sa 4-bitnom lijevom polovicom ključa u prvom ciklusu, a zatim se miješa sa 4 bitnom desnom polovicom ključa u drugom ciklusu. Postoji samo 256 mogućih ključeva i 16 parova mogućih ulaza odnosno pripadajućih izlaza. To znači da se svaki od 16 parova (par čini ulaz i njegov pripadajući izlaz), može dobiti korištenjem različitih ključeva. Trik je u pronalaženju ispravnog ključa koji će učiniti istu akciju za sve poznate parove. Uočite da se kriptosustav na slici ispod neznatno promijenio u odnosu na početnu sliku kriptosustava.

Kriptosustav kriptiran jednostavnom zamjenom - izmjenjeni Izvor

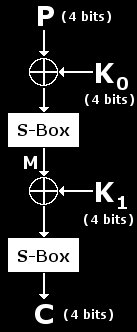
U daljnjem tekstu više neće biti spominjane lijeva i desna polovica ključa. Lijeva polovica ključa je sada K1, a desna K2 te je svaki od njih veličine 4 bita. Ovi dijelovi originalnog ključa poznati su kao podključevi i predstavljaju metu samog napada. Oporavkom K1 i K2 također će se oporaviti i originalni ključ. Središnja točka između prvog i drugog ciklusa označena je s M te je ta vrijednost još uvijek nepoznata. Zasada je M istovremeno izlaz iz 1. kruga i ulaz u 2. krug. Što se tiče S-blokova oba su identična iako to nije nužno, ali olakšava shvaćanje i samu implementaciju. Slika ispod predstavlja sadržaj S-blokova. Na lijevoj strani prikazani su ulazi, a odgovarajući izlazi na desnoj strani odnosno iza ->

S-blok kriptosustava Izvor

Linearne aproksimacije

Slučajno se može dogoditi da se pogodi dio originalnog ključa – K0, a isto tako i da se pogodi M. Pošto imamo samo originalni tekst (P) i šifrirani tekst (C) , a M je nepoznat, pitanje je kako znati da li je pretpostavljeni M ispravan. Ne postoji način kako saznati da je pretpostavljeni M sigurno točan (bez brute force napada), ali postoji način kako naučiti pogoditi. Čak ne treba imati nikakve informacije o K1 da bi se to dogodilo. Važno je znati, zašto je potvrda točnosti M važna za napadača. Ukoliko postoji 90% sigurnost da je M točan nakon nagađanja K0, šifriranje se može pokrenuti unatrag kroz S-blok te izvršiti xor operaciju sa pretpostavljenim M što nam daje dobar pogodak K1. Ovaj naučeni postupak za pogađanje ključa, može se primijeniti na šifrirani tekst i testirati nad svim poznatim parovima. Ako su svi parovi koristeći K0 i K1 kriptirani ispravno, tada su pretpostavke točne i napadač pobjeđuje.

Linearnost je težak i dvosmislen pojam za shvatiti. Umjesto toga laički će biti objašnjeno shvaćanje tog pojma. Ako se u „čarobnu kutiju“ dodaju slučajne vrijednosti i ako se odgovarajuća vrijednost može pretpostaviti vađenjem bilo koje vrijednosti iz kutije, čarobna kutija je zapravo nešto linearno. Na primjer zamislit ćemo da se u kutiji nalazi ulazna vrijednost kojoj pridodajemo broj jedan. Vrijednost koju tražimo ovisi o tome da li je ulazna/izlazna vrijednost paran broj. Drugim riječima dodavanje jedinice parnom broju rezultira neparnim brojem i obrnuto. Stoga će čarobna kutija biti potpuno linearna u odnosu na djeljivost s brojem 2. Gornji način razmišljanja nije u potpunosti točan, ali pomaže u razumijevanju koncepta pogotovo jer se odnosi na linearnu kriptoanalizu.

S-blokovi su jedini nelinearni dijelovi šifre. Idealno je da S-blok primi ulaznu vrijednost sa vjerojatnošću X, a da izlaz bude vrijednost sa vjerojatnošću Y koja je zapravo 50% od ulazne vjerojatnosti. Svojstvo koje će dalje spominjati je paritet. To je logička (eng. boolean) vrijednost (1 ili 0) koju dobijemo upotrebom xor operacije na neke bitove. Bitovi na kojima je izvršena xor operacija definiraju novi broj nazvan maskom (eng. mask).

Prikaz ulaznih i izlaznih maski Izvor

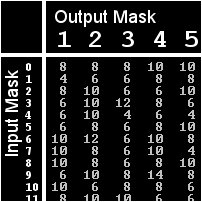
Koncept maskiranja koristit će se za pronalaženje linearnosti S-blokova. Testirat će se svaka pojedina kombinacija ulazne maske u odnosu na izlaznu masku. Isto će biti i za svaki mogući 4-bitni ulaz. U osnovi će se uzimati ulazna vrijednosti koja se maskira korištenjem ulazne maske. Rezultat tog postupka maskiranja zvati će se ulazni bit. Nadalje će se uzimati originalni ulaz i proći će kroz S-blok, a zatim će se biti maskiran sa izlaznom maskom. Zatim se uspoređuje izlazni paritet sa ulaznim. Ako su pariteti međusobno isti, potvrđuje se da je kombinacija ulaznih i izlaznih maski točna za taj ulaz. Nakon provedenog postupka za svaki mogući par ulazno/izlaznih maski, dobije se tablica linearne aproksimacije. Svaki redak u tablici predstavlja broj koliko je puta linearna aproksimacija postignuta za određeni par ulazno/izlaznih maski kada se uspoređuju sa svih 16 mogućih ulaza. Kada bi S-blok potpunosti bio nelinearan, svaki ulaz bio bi 8 te bi provođenje linearne kriptoanalize bilo nemoguće.

Najbolja aproksimacija?

Sad kada postoji tablica brojeva i njima pridruženim maskama, zamislit će se da jedna od gornjih aproksimacija u tablici čita broj 16 (Slika: Prikaz ulaznih i izlaznih maski. To bi značilo da je iskorišteno 100% vremena. Drugim riječima, ako punimo S-blok ulazima, njegov ulazni paritet odgovarat će maskiranom izlaznom paritetu nakon prolaska kroz S-blok. Treba spomenuti da ovdje xor operacija nema nikakvog utjecaja. Ako se nad ulazom izvrši xor operacija sa brojem 1 prije maskiranja, za posljedicu može imati aproksimaciju u kojoj je iskorišteno 0% vremena umjesto 100%. Jedna dobra linearna aproksimacija za S-blok kriptosustava je 11->11 koja sadrži 14 od 16 ulaza.

Točna aproksimacija za 14 od 16 ulaza Izvor

Drugim riječima, ako se izvrši xor operacija nad bitovima 1, 2 i 4 za gotovo sve ulaze, ta vrijednost biti će jednaka pridruženom izlaznom paritetu, naravno koristeći istu masku u ovom slučaju. Ova činjenica ne će vrijediti za samo 2 ulaza. Ako je nad tim ulazima prvo provedena xor operacija s podključem, vjerojatnost istinitosti biti će 2/16.

Testiranje središnje točke

Prisjetimo se da se nakon nagađanja K0, može testirati M. M će se gledati kao ulaz u drugi ciklus. U drugom ciklusu je izvršena xor operacija s ključem K1 koja zapravo ne utječe na vjerojatnosnu točnost linearne aproksimacije. Sada na red dolazi S-blok koji je maloprije aproksimiran. Koristit će se pretpostavljeni ulaz i koristiti ulazna maska 11 kako bi dobili paritet. Zatim će se uzeti pripadajući stvarni izlaz iz drugog ciklusa (poznati šifrirani tekst) i maskiranjem s 11 dobit će se paritet. Ako su pretpostavljeni pariteti jednaki realnim izlaznim paritetima, za oko 14 od 16 ili 2 od 16 poznatih parova, K0 korišten za generiranje M vrijednosti je točan. Važno je primijetiti da se ne obraća pažnja na to kako je generiran M, već da li je pogođeni K0 za njegovo dobivanje. Sadržaj S-blokaiz prvog ciklusa nije važan te nije testirana linearna aproksimacija nad njom. Samo se svojstva S-bloka iz drugog ciklusa koriste za testiranje točnosti pretpostavljenog M-a. Ukoliko pretpostavljeni K0, a time i M nisu točni, linearna aproksimacija ne će biti jednaka kao i stvarna. Zapravo su se koristili poznati izlazi te su testirani s pretpostavljenim ulazima. Linearna aproksimacija je ta koja omogućava da se nauči pogađati/pretpostavljati da je određeni ulaz generirao baš taj izlaz. Pretpostavljeni K0 je točan, ako se linearna aproksimacija slaže sa stvarnom vjerojatnošću. Sad kad su poznati P, K0, M i C, trivijalno se dobiva i K1. Dovoljno je uzeti C, vratiti ga unatrag kroz S-blok, izvršiti xor operaciju sa poznatim M. Rezultat će biti K1 koji u kombinaciji sa K0 daje originalni ključ. Zatim se testira originalni ključ nad svakim poznatim otvorenim tekstom kako bi se vidjelo da li se generira pripadajući šifrirani tekst. Ako je generiranje točno, originalni ključ je pronađen.

Koliko je dobra metoda linearne kriptoanalize?

Kao mjerilo uzeto je koliko se ciklusa koristi. Testiranjem svakog ključa nad 16 poznatih parova (otvoreni/šifrirani tekst) daje 256*16*2 (2 su ciklusa) mogućnosti. Obično se za napad linearnom kriptoanalizom uzimaju 2 kandidata za K0, ako ih je više, potrebno je testirati svaki nad svim poznatim parovima kako bi se dobila pretpostavka za M. Za računanje K0 postoji 16*16 mogućnosti. Zatim se testira svaki kandidat (pretpostavili smo da imamo 2) nad svim poznatim parovima. To dodaje 2*2*16 mogućnosti (2 ciklusa, 2 kandidata, 16 parova). Znači linearna kriptoanaliza s obzirom na broj korištenih slučajeva (ovdje su 2), posjeduje sveukupno 16*16+16*2*2 mogućnosti. Drugo mjerilo je koliko mogućnosti postoji za pronalazak ključa. Linearna kriptoanaliza obično pronalazi ključ testirajući 300 mogućnosti. Maksimum mogućnosti proizlazi iz broja kandidata za ključ K0. Za dva kandidata K0 maksimum je 320. No, to ne funkcionira baš samo tako jer se ponekad uopće ne pronađe točan ključ. Neka osnovna istraživanja, pokazuju da se u 80% slučajeva provođenjem linearne kriptoanalize pronalazi ključ. Prema

Primjer koda J. Kinga napisan u jeziku C, predstavlja implementaciju kriptosustava kriptiranog jednostavnom zamjenom. Unutar se izračunava aproksimacija, koristi se linearna kriptoanaliza za pronalaženje ključa i nakraju se vidi usporedba računske složenosti u odnosu na brute force napad.

Primjer linearne kriptoanalize (S-DES)

Kroz sljedeći primjer, koji je dio rada jednog Sveučilišta iz Arizone [11], pokušat će se prikazati i objasniti na koji način radi linearna kriptoanaliza pomoću S-DES (Simplified – Data Encryption Standard).

Najprije treba definirati funkciju f koja kao ulazne parametre uzima 8-bitni ulaz (x) i 8-bitni podključ (k), a kao rezultat daje 8-bitni izlaz (y). Možemo to sada zapisati kao izraz y = f(x, k) (mod 2). Ako se pokuša zamisliti funkciju f kao linearnu kombinaciju x i k mod 2, tada bi funkcija f izgledala kao izraz y = f(x, k) = Mx + Dk (mod 2), pri čemu M i D predstavljaju matrice dimenzija 8 x 8. Na sljedećoj slici može se i jasno vidjeti takav zapis:

Da bi se omogućio takav zapis, potrebno je izmijeniti S-boxove u linearne funkcije, dok su sve permutacije i XOR operatori već linearne funkcije. Primjerice, P4 se može zapisati kao y = h(x):

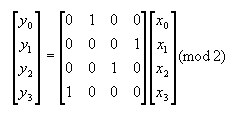
XOR4 se može zapisati kao z = i(x, y):

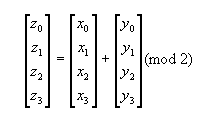
Dakle, ako bi S-blokovi bili linearne funkcije, vrlo lako bi se mogla pronaći linearna funkcija y = f(x, k) (mod 2). SW switch funkcija je također permutacija pa je samim time i linearna funkcija. Stoga, može se zapisati kao y = g(x) = Ex gdje je E matrica dimenzije 8x8:

S - DES ima dva obilaska funkcije f (po jedan za svaki podključ K1 i K2) sa SW switch funkcijom između. Dakle, ako je P otvoren tekst i C je šifriran tekst uz ignoriranje početne i završne permutacije, vrijedi sljedeće:

C=f(g(f(P, K1)), K2)
 =M' g(f(P, K1)) + D' K2
 =E' M' f(P, K1) + D' K2
 =E' M' (M' P + D' K1) + D' K2
 =E' M2' P + E' M' D 'K1 + D 'K2 (mod 2)

Sada je potrebno definirati tri nove 8x8 matrice:

  • R = E' M2, 
  • S = E' M' D, i
  • T = D.

Čak i ako se koriste nezavisni podključevi za K1 i K2, i dalje je to linearna jednadžba C = R' P + S' K1 + T' K2 (mod 2). Nadalje, možemo dobiti ovakvu linearnu jednadžbu za bilo koji broj obilazaka. Uzmimo za primjer četiri obilaska gdje su K1, K2, K3 i K4 svi neovisno odabrani podključevi koji nisu generirani od strane istog ključa za šifriranje:

  C = R' P + S' K1 + T' K2 + U' K3 + V' K4 (mod 2).

Svaki element u R, S, T, U i V je ili 0 ili 1. To znači da je i dotični bit u P, K1, K2, K3, K4 prisutan u jednadžbi za šifrirani tekst ili 0 ili 1. Dakle, vjerojatno će se dobiti nešto poput:

  C0 = P3 + P4 + P5 + K10 + K12 + K13 + K15 + ... + K45 + K47.

To nam govori da je bit 0 šifriranog teksta jednak bitu 3 otvorenog teksta XOR-anog s bitom 4 otvorenog teksta, XOR-anog sa bitom 5 otvorenog teksta, XOR-anog sa bitom 0 K1., itd. Imali bismo slične jednadžbe za bitove 1 do 7 šifriranog teksta. Tako bismo primjerice za neki „napad“ na šifrirani tekst s jednim šifrirano – otvorenim parom teksta imali 8 jednadžbi i 32 nepoznanice, što nam i nije od neke koristi. Međutim, s 4 šifrirano – otvorenim parovima teksta, imali bismo 32 jednadžbe i 32 nepoznanice. Koristeći Gaussov postupak ili Cramerovo pravilo, vidimo da bismo taj sustav jednadžbi mogli riješiti s 32 izračuna. Ako bismo došli do toga da 2 ili više jednadžbi nisu linearno nezavisne, možemo jednostavno dodati još jedan par šifrirano – otvorenog teksta. Dakle, veličina ključa od 32 bita nam u ovom slučaju daje nam kriptoanalitičku složenost od 32 umjesto 2³² koliko bismo se nadali u slučaju nekoliko poznatih parova. Srećom, S-DES i DES koriste S-blokove koji su nelinearni. Međutim, to ne znači da se linearna jednadžba funkcije f neće održati za neke parove ulaza i izlaza. U idealnim uvjetima, linearna jednadžba (mod 2), održati će se za bilo koji par ulaza i izlaza u točno 50% slučajeva. To je tako iz razloga što primjerice da uzmete nasumično odabrane bitove i stavite ih u linearnu jednadžbu (mod 2), očekivat ćete da u 50% slučajeva dobijete 0 kao rezultat, a u 50% slučajeva 1 kao rezultat.

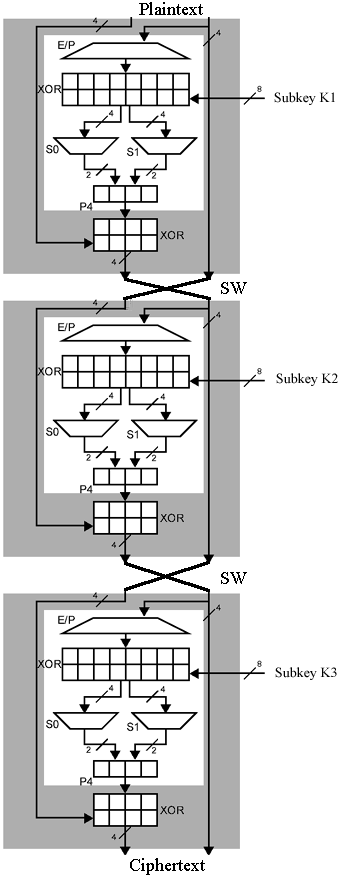
Pokušajmo sada proći korak po korak kroz linearnu kriptoanalizu na modificiranom S-DESu koja ima 3 obilaska umjesto 2, koristi 3 nezavisna podključa (K1, K2 i K3) i nema inicijalnu ili završnu permutaciju (iz razloga što te permutacije ionako ne čine previše).

  1. KORAK:

Potrebno nam je otprilike 16 dobrih linearnih aproksimacija za svaki S-blok. Te aproksimacije bi se trebale održati za više od 50% mogućih ulaza za S-blok. Svaka jednadžba uzima nekoliko bitova od ulaza i nekoliko od izlaza S-bloka i zbraja ih zajedno (mod 2), što je ekvivalentno XOR-anju, kako bismo dobili 0 ili 1 kao rezultat. Bit će potrebno oko 8 jednadžbi za S0 i još oko 8 za S1.

  2. KORAK:

Potrebno nam je i oko 100 parova otvoreno-šifriranog teksta. Ne moraju biti odabrani kao otvoren tekst, ovo je poznati napad na otvoren tekst.

  3. KORAK:

Ponavljati korak 4 za svaki podključ K3 koji je moguć.

  4. KORAK:

Korak 4 se sastoji od više dijelova, a podrazumijeva da za svaki par otvoreno-šifriranog teksta koji imamo:

  • 4.1:

Pronaći Q, rezlultat S-blokova nakon 2. obilaska. U ovom modificiranom S-DESu koji se sastoji od 3 obilaska, takvo što ne bi trebalo predstavljati problem. XOR4 je u drugom obilasku uzeo desnu polovicu otvorenog teksta kao ulaz (budući da u prvom obilasku nije doticao desnu polovicu otvorenog teksta) i prikazao desnu polovicu šifriranog teksta kao izlaz (budući da u trećem obilasku nije doticao desnu stranu šifriranog teksta). Ukoliko XOR-amo to dvoje, trebali bismo dobiti još jedan ulaz u drugi obilazak XOR4. I tada je još samo potrebno napraviti inverz od P4 kako bismo saznali koji je bio razultat S-boxova za drugi obilazak.

  • 4.2:

Pronaći S, ulaz u XOR8 u drugom obilasku. To možemo napraviti na način da uzmemo desnu polovicu šifriranog teksta i koristeći ju kao ulaz u E/P u trećem obilasku. Možemo samo uzeti podključ K3 koji trenutno isprobavamo i napraviti XOR8, S-blokove i P4 za treći obilazak. Izlaz koji dobijemo od P4 i lijeva polovica šifriranog teksta su jedan ulaz i izlaz za XOR4. Potrebno je samo XOR-ati to dvoje kako bismo dobili drugi input za XOR4 u trećem obilasku. Možemo i pratiti ovaj ulaz natrag i vidjeti da je to isto kao i ulaz u E/P u drugom obilasku. Samo ga priključimo u E/P u drugom obilasku i imamo S.

  • 4.3:

Vidjeti da li se svaka od naših linearnih aproksimacija održava za S kao ulaz i Q kao izlaz. Zapravo nas ne zanima kakav je podključ K2 iz razloga što svaki bit u K2 ima 50% šanse biti 0 i ne dodirivati ništa. Da je kojim slučajem 1, onda bi promijenio jedan od bitova u S, ali naše linearne aproksimacije svejedno i dalje imaju postotak sklonosti od 50%. Ako je S dobro odabran (što znači da smo dobro pretpostavili K3), onda bismo očekivali da S i Q pokažu sklonost linearnim aproksimacijama. Ako S nije kao ulaz koji se stvarno koristio prilikom generiranja parova otvoreno-šifriranih tekstova, onda se priključuju nasumični bitove za S i Q očekujući da će se naše linearne aproksimacije održati u 50% slučajeva. Podključ za koji pretpostavljamo da pokazuje najveću razliku od 50% je onaj koji je najvjerojatnije pravi K3. Ako nije, onda je pravi K3 definitivno drugi ili treći na listi.

Važna stvar za primijetiti jest da kada jednom znamo K3, možemo na isti način napasti i K1 i K2. Razina složenosti za razbiti šifru tada dolazi od veličine podključa, a ne veličine ključa. O(2⁸) za razbiti K3 + O(2⁸) za razbiti K2 + O(2⁸) za razbiti K1 znači ukupnu složenost O(2⁸). Dolazimo do zaključka da je ovo poprilično jednostavnije od brute force napada na 24-bitni ključ čija bi složenost tada bila O(2²⁴). Naravno da linearna kriptoanaliza neće proizvesti ovako „dramatične“ rezultate na pravom DES-u jer koristi 16 obilazaka i mnogo bolji S-box dizajn. Stupanj složenosti linearne kriptoanalize kod pravog DES-a i dalje ovisi o veličini podključa, ali je jednostavno neisplativa.

Linearni napad

S kutije ovise o relativno malom broju bitova. Točnije 6 bitova, koji omogućuju da se zapišu linearno povezani izrazi kako bi se S kutija aproksimirala. Kako se utjecaj runde ne rasprši brzo preko druge runde, linearni povezani izrazi koji drže po različitim rundama se mogu kombinirati kroz runde. Ukoliko imamo Pi kao ne kriptirane bitove teksta, Ci kao kriptirane bitove teksta i Ki kao bitove pod ključa, želimo naći izraz sljedeće forme.

Za takav izraz želimo da ima ili veliku ili malu mogućnost pojavljivanja. Ukoliko bi baš toliko očiti izraz postojao, on bi nam označavao da je kriptiranje jako slabo. Ukoliko bi pak nasumično odabrali bitove za gornji izraz, on bi ih trebao sadržavati točno 1/2 puta. No, naš je cilj naći izraz koji ima ili veliku ili malu mogućnost pojavljivanja. Ako pronađemo izraz koji sadrži puno veću ili puno manju frekvenciju pojavljivanja, onda ga možemo iskoristiti.[Prema 23]

Linearni napad na DES (4 runde)

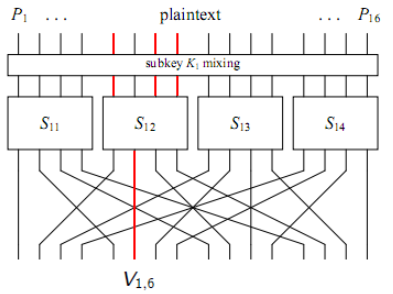
Prvi korak je da moramo pronaći neku linearnu aproksimaciju za S kutiju koju koristi DES algoritam. Podsjetimo se, S kutije u DES algoritmu koriste 6 bitova kao ulaz, dok na izlazu daju 4 bita. Pronašli smo aproksimaciju koja ima odstupanje približno jednako 0.31.

Kako pratimo izraz kroz f funkciju DES algoritma, dobivamo sljedeće.

Koristeći Pilling up princip za aproksimaciju pete S kutije, na kraju dobivamo sljedeći izraz.

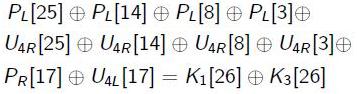
Odstupanje za ovaj izraz je približno 0.3, te nam to ujedno i predstavlja najbolji izraz za DES sa 3 runde. Napad se izvršava tako da se vrati zadnja runda. Na kraju, ukoliko smo dobro pogodili 6 djelomični bitova pod ključa, jednadžba za 3 runde će održati veliko odstupanje koje je imala, u suprotnom će se to odstupanje približiti nuli.

Iako nam ovaj napad otkriva samo 6 bitova od 56 bitnog ključa, puno je lakše i brže pronaći ključ u 2⁵⁰ mogućih kombinacija nego u 2⁵⁶ mogućih kombinacija.

Koristeći Matsui Lemmu 5, može se izračunati broj nasumičnih potrebnih ne kriptiranih i kriptiranih parova teksta kako bi šanse za otkrivanje ključa bile skoro 100%. Konkretno u našem primjeru imamo DES reduciran na 4 runde. Prema navedenom izračunu za potpuni uspjeh otkrivanja ključa trebali bi imati 256 parova teksta.

Za potpuni DES algoritam, odnosno za svih 16 rundi, potrebno je 2⁴⁷ parova teksta kako bi uspjeh otkrivanja bio skoro 100%.[Prema 23]

Literatura

1. Stamp M. (2006). Information Security principles and practice. Dostupno 19.1.2013. na: http://www.google.hr/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=0CCkQFjAA&url=http%3A%2F%2Fbkitsec.googlecode.com%2Ffiles%2FInformation%2520Security.pdf&ei=ibv6UJSBG4bhtQaAtIHQAg&usg=AFQjCNF9wFeB1GsmxK10M-5zG0uBPogz3g&bvm=bv.41248874,d.bGE

2. CCERT (2009). Kriptoanaliza. Dostupno 19.1.2013. na: http://www.cert.hr/sites/default/files/CCERT-PUBDOC-2009-08-275.pdf

3. CCERT (2003). DES algoritam. DOstupno 19.1.2013. na: http://www.cis.hr/www.edicija/LinkedDocuments/CCERT-PUBDOC-2003-06-24.pdf

4. Baigneres T., Junod P., Vaudenay S. (-) How Far Can We Go Beyond Linear Cryptanalysis?. Dostupno 19.1.2013. na: http://www.google.hr/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&cad=rja&ved=0CDEQFjAB&url=http%3A%2F%2Fciteseerx.ist.psu.edu%2Fviewdoc%2Fdownload%3Fdoi%3D10.1.1.73.6%26rep%3Drep1%26type%3Dpdf&ei=97r6ULm4MqOA4gTru4GACg&usg=AFQjCNHJfdciYMBTkFpUH7XmPvyzu4fhAw&bvm=bv.41248874,d.bGE

5. Poljak D. (2005). Kriptoanaliza. Dostupno 19.1.2013. na http://os2.zemris.fer.hr/algoritmi/simetricni/2005_poljak_darko/seminar/doc/seminar.pdf

6. Howard M. Heys (-) A Tutorial on Linear and Differential Cryptanalysis. Dostupno 19.1.2013. na http://www.engr.mun.ca/~howard/PAPERS/ldc_tutorial.pdf

7. Dujella A. (-) Klasična kriptografija. Dostupno 19.1.2013. na http://web.math.pmf.unizg.hr/~duje/kript/osnovni.html

8. Meissler D. (2012). The Difference Between Encoding, Encryption, and Hashing. Dostupno 19.1.2013. na: http://danielmiessler.com/study/encoding_encryption_hashing/

9. Galinović A. (2005). Povijest kriptografije. Dostupno 19.1.2013. na: http://web.zpr.fer.hr/ergonomija/2005/galinovic/PovijestKriptografije.pdf

10. elitesecurity (2011). Sve o kriptografiji (za početnike). Dostupno 19.1.2013. na: http://arhiva.elitesecurity.org/t424669-Sve-kriptografiji-za-pocetnike

11. Embry-Riddle Aeronautical University in Prescott, Arizona (2002). Linear Cryptanalysis Demo. Dostupno 18.1.2013. na http://nsfsecurity.pr.erau.edu/crypto/lincrypt.html

12. ZSIS. (2009). Kriptografija. Dostupno 15.1.2013. na: http://www.zsis.hr/site/Kriptografija/tabid/126/Default.aspx

13. MSDN. (2012). Data Confidentiality. Dostupno 15.1.2013. na: http://msdn.microsoft.com/en-us/library/ff650720.aspx

14. InfoSec Institute. (2009). Symmetric Cryptography. Dostupno 15.1.2013. na: http://www.symmetriccryptography.com/

15. CCERT. (2003). IDEA algoritam. Dostupno 16.1.2013. na: http://www.cis.hr/www.edicija/LinkedDocuments/CCERT-PUBDOC-2003-06-25.pdf

16. Anonimus. (2012). International Data Encryption Algorithm. Dostupno 16.1.2013. na: http://en.wikipedia.org/wiki/International_Data_Encryption_Algorithm

17. Savard, J. (1999). A Cryptographic Compendium. IDEA (International Data Encryption Algorithm). Dostupno 16.1.2013. na: http://www.quadibloc.com/crypto/co040302.htm

18. Savard, J. (1999). A Cryptographic Compendium. The Advanced Encryption Standard (Rijndael). Dostupno 17.1.2013. na: http://www.quadibloc.com/crypto/co040401.htm

19. Anonimus. (2013). Advanced Encryption Standard. Dostupno 18.1.2013. na: http://en.wikipedia.org/wiki/Advanced_Encryption_Standard

20. CCERT. (2003). AES algoritam. Dostupno 18.1.2013. na: http://www.cis.hr/www.edicija/LinkedDocuments/CCERT-PUBDOC-2003-08-37.pdf

21. King J. (-). Linear Cryptanalysis Tutorial. Dostupno 19.1.2013. na: http://www.theamazingking.com/crypto-linear.php

22. J. Orlin Grabbe (-). The DES Algorithm Illustrated. Dostupno 20.1.2013. na http://page.math.tu-berlin.de/~hess/krypto-ws2006/des.htm

23. Slava Chernyak, Sourav Sen Gupta (2009) Linear and Differential Cryptanalysis of DES. Dostupno 20.01.2013. na http://chernyak.com/files/destalk.pdf

Doprinosi

Iva Kiš - Povijest linearne kriptoanalize; Općenito o linearnoj kriptoanalizi; Pregled osnovnog napada linearne kriptoanalize; Linearna kriptoanaliza kriptosustava kriptiranog jednostavnom zamjenom (eng. toy cipher)

Nikola Pavetić - Kriptiranje; Kriptiranje i kodiranje; Povijest kriptografije; Najpoznatiji načini kriptiranja kroz povijest; Hijeroglifi; Hebrejska šifra; Skital; Cezarova šifra; Polybiusov kvadrat; Kriptoanaliza; Povijest kriptoanalize; Klasična kriptoanaliza; Moderna kriptoanaliza; Linearni napad; Linearni napad na DES (4 runde)

Jurica Sugnetić: DES algoritam (Data Encryption Standard); Kako radi DES?; Matematička pozadina linearne kriptoanalize; Jednostavna supstitucijsko-permutacijska mreža

Anita Završki: Simetrična kriptografija; IDEA algoritam (International Data Encryption Algorithm); AES algoritam (Advanced Encryption Standard)

Antonio Zrinušić: Primjer linearne kriptoanalize (S-DES)